In these lessons, we will learn
- the concept of inequalities and the symbols used.
- linear inequalities in one variable
- how to graph inequalities on the number line.
We also have an inequalities calculator that can graph inequalities on a number line. Use it to check your answers.
The Concept Of Inequalities
An inequality is a relationship between two quantities that are not equal.
The symbols used for inequality are:
> means ‘greater than’
< means ‘less than’
≥ means ‘greater than or equal to’
≤ means ‘less than or equal to’
Linear Inequality In One Variable
In equations, one side is equal to the other side. In linear inequalities, one side is bigger than or smaller than or equal to the other side.
A linear equation in one variable has only one solution. An inequality in one variable has a set of possible solutions.
Example:
Given that x is an integer. State the possible integer values of x in the following inequalities.
a) x > 4
b) x ≤ –3
Solution:
a) x is greater than 4.
5, 6, 7, 8, …
b) x is less than or equal to –3
–3, –4, –5, –6, …
Using The Number Line To Represent Inequalities
We can represent a linear inequality in one variable on a number line. We use the following symbols in the representation.
A small circle ⚬ is used for < and > to indicate that the number is not included.
A filled-in circle • is used for ≤ and ≥ to indicate that the number is included.
A line with an arrow indicates that the line continues to infinity in the direction of the arrow.
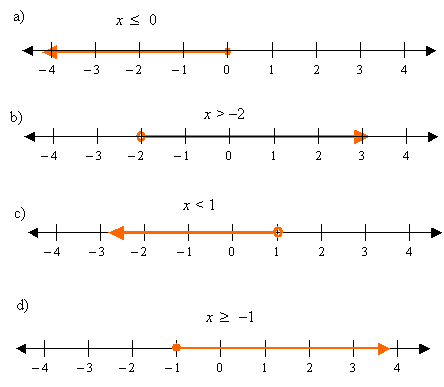
Example:
Represent each inequality on a number line.
a) x ≤ 0
b) x > 2
c) x < 1
d) x ≥1
Solution:
Inequalities on a number line
How to plot an inequality on a number line?
Example:
Graph x < 4
Graphing Inequalities on a Number Line
Example:
Solve and graph the following inequalities:
a) 3x + 2 > 5
b) x - 5 ≤ 6
c) 2/3 x + 4 ≥ 5
d) -4x + 2 ≤ 10
e) x/-3 + 1 > 4
f) 2x - 8 < 0
Introduction to Linear Inequalities
How to Graph an Inequality on a Number Line?
Examples:
x = 2
x < 2
x < 2
x > -1
x ≥ -1
2 < x
-3 ≥ x
-2 ≤ x < 1
How to write inequalities from a number line?
This inequalities calculator will graph inequalities on the number line.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.