Introduction to Exponential Functions
Examples, solutions, videos, worksheets, and activities to help PreCalculus students learn about exponential functions.
What is an exponential function?
An exponential function f is given by
f(x) = bx,
where x is any real number, b > 0 and b ≠ 1.
The number b is called the base.
If b > 1, f(x) is a positive, increasing, continuous function. In this case, f(x) is called an exponential growth function.
if 0 < b < 1, f(x) is a positive, decreasing, continuous function. In this case, f(x) is called an exponential decay function.
The following diagram compares the graphs of exponential functions. Scroll down the page for more examples and solutions on the graphs of exponential functions.
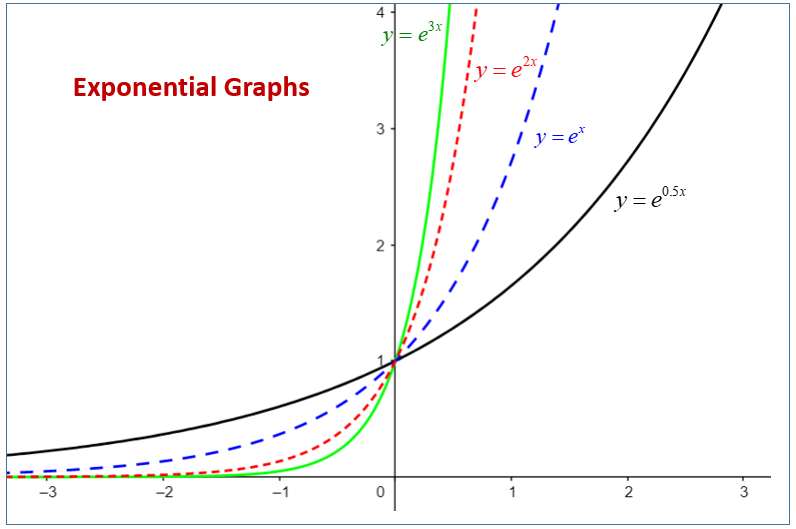
Graphs of Exponential Functions
We often encounter exponential functions in science and mathematics. Exponential functions have a unique set of characteristics and asymptotic behavior that make their graphs recognizable. It is important to be able to recognize the graphs of exponential functions, the graphs of their inverses (logarithmic functions) and to know properties that help us solve equations with exponents and logs.
Graph Exponential Functions
Graphing Exponential Functions
This video shows how to graph two exponential functions by plotting points, discuss the domain and range and asymptotes as well as 4 extra graphs using transformations.
An Introduction to Graphing Exponential Functions
Exponential Functions Introduction
The video introduces exponential functions by contrasting them to linear and quadratic functions. It shows growth and decline functions, giving examples in nature. Examples shown are in population growth, half life, and musical tones.
Graphing Exponential Functions
Example:
Graph y = 5x
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.