Horizontal And Vertical Graph Stretches And Compressions
These lessons with videos and examples help Pre-Calculus students learn about horizontal and vertical graph stretches and compressions.
Related Pages
Graphs Of Functions
Parent Functions And Their Graphs
Transformations Of Trigonometric Graphs
More Pre-Calculus Lessons
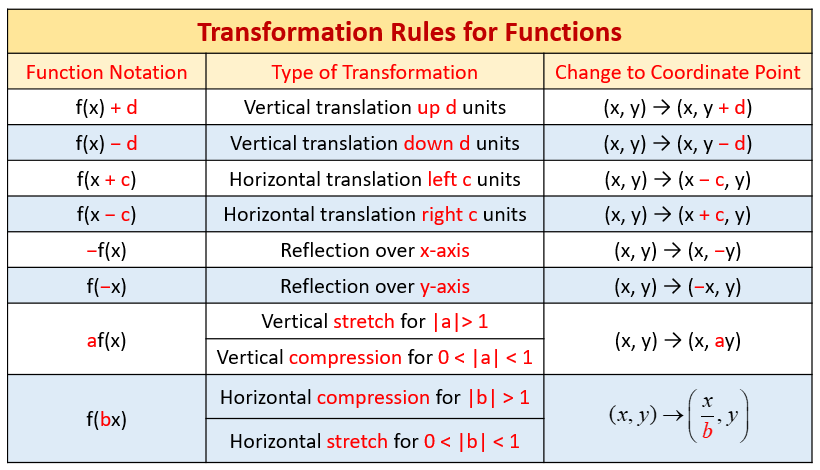
The following table gives a summary of the Transformation Rules for Graphs. Scroll down the page for more examples, solutions and explanations.
Function Transformations: Horizontal And Vertical Translations
This video explains to graph graph horizontal and vertical translation in the form af(b(x-c))+d.
It looks at how c and d affect the graph of f(x).
Function Transformations: Horizontal And Vertical Stretch And Compression
This video explains to graph graph horizontal and vertical stretches and compressions in the
form af(b(x-c))+d.
It looks at how a and b affect the graph of f(x).
Horizontal And Vertical Graph Stretches And Compressions (Part 1)
The general formula is given as well as a few concrete examples.
- y = c f(x), vertical stretch, factor of c
- y = (1/c)f(x), compress vertically, factor of c
- y = f(cx), compress horizontally, factor of c
- y = f(x/c), stretch horizontally, factor of c
- y = - f(x), reflect at x-axis
- y = f(-x), reflect at y-axis
Horizontal And Vertical Graph Stretches And Compressions (Part 2)
This video discusses the horizontal stretching and compressing of graphs.
Graph Transformations About The X-Axis And Y-Axis
This video talks about reflections around the X axis and Y axis.(Part 3)
Effects On The Parent Function
In this video we discuss the effects on the parent function when:
- Stretched Vertically,
- Compressed Vertically,
- Stretched Horizontally,
- Compressed Horizontally.
Different Types Of Math Transformation
There are different types of math transformation, one of which is the type y = f(bx). This type of math transformation is a horizontal compression when b is greater than one. We can graph this math transformation by using tables to transform the original elementary function. Other important transformations include vertical shifts, horizontal shifts, and reflections.
This video reviews function transformation including stretches, compressions, shifts left, shifts right, and reflections across the x and y axes.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.