Math Work Problems - Two Persons
In these lessons, we will learn how to solve work problems that involve two persons who may work at different rates.
Related Pages
Work Problems
Solving Work Word Problems Using Algebra
More Algebra Lessons
Work Problems are word problems that involve different people doing work together but at different rates. If the people were working at the same rate then we can use the Inversely Proportional Method instead.
How To Solve Work Problems: Two Persons, Unknown Time
We will learn how to solve math work problems that involve two persons. We will also learn how to solve work problems with unknown time.
The following diagram shows the formula for Work Problems that involve two persons. Scroll down the page for more examples and solutions on solving algebra work problems.
This formula can be extended for more than two persons.
"Work" Problems: Two Persons
Example:
Peter can mow the lawn in 40 minutes and John can mow the lawn in 60 minutes. How long will it take for
them to mow the lawn together?
Solution:
Step 1: Assign variables:
Let x = time to mow lawn together.
Step 2: Use the formula:
Step 3: Solve the equation
The LCM of 40 and 60 is 120
Multiply both sides with 120
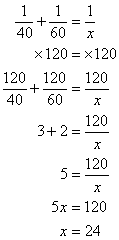
Answer: The time taken for both of them to mow the lawn together is 24 minutes.
Work Problems With One Unknown Time
Examples:
- Catherine can paint a house in 15 hours. Dan can paint a house in 30 hours. How long will it take them working together.
- Evan can clean a room in 3 hours. If his sister, Faith helps, it takes them two and two-fifths hours. How long will it take Faith working alone?
Variations Of GMAT Combined Work Problems
Examples:
- Working at a constant rate, Joe can paint a fence in 4 hours. Working at a constant rate, his brother can paint the same fence in 2 hours. How long will it take them to paint the fence if they both work together at their respective constant rates?
- Working alone at a constant rate, machine A takes 2 hours to build a care. Working alone at a constant rate, machine B takes 3 hours to build the same car. If they work together for 1 hour at their respective constant rates and then machine B breaks down, how much additional time will it take machine A to finish the car by itself?
- Working alone at a constant rate, Carla can wash a load of dishes in 42 minutes. If Carla works together with Dan and they both work at constant rates, it takes them 28 minutes to wash the same load of dishes. Working at a constant rate, how long would it take Dan to wash the load of dishes by himself?
How To Solve “Working Together” Problems?
Example:
It takes Andy 40 minutes to do a particular job alone. It takes Brenda 50 minutes to do the same job
alone. How long would it take them if they worked together?
Word Problem: Work, Rates, Time To Complete A Task
We are given that a person can complete a task alone in 32 hours and with another person they can finish the task in 19 hours. We want to know how long it would take the second person working alone.
Example:
Latisha and Ricky work for a computer software company. Together they can write a particular computer
program in 19 hours. Latisha van write the program by herself in 32 hours. How long will it take Ricky
to write the program alone?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.