Perfect Cubes And Cube Roots
Related Pages
More Lessons For Grade 8
Perfect Squares
Math Worksheets
In these lessons, we will learn what are perfect cubes and how to calculate the cube root of a perfect cube.
What Is A Perfect Cube?
A perfect cube is a number that is the cube of an integer.
For example, 125 is a perfect cube since 125 = 5 × 5 × 5 = 53
Some other examples of perfect cubes are 1, 8, 27, 64, 125, 216, 343, …
What Is A Cube Root?
The opposite of cubing a number is finding the cube root. Since 53 = 125, the cube root of 125 is 5. The cube root of a perfect cube is an integer.
It is possible to get the cube root of a negative number. For example, the cube root of −125 is −5 since (−5) × (−5) × (−5) = −125.
The following table shows perfect cubes from 1 to 1000 and their corresponding cube roots. Scroll down the page for more examples of how to evaluate cube root of perfect cubes.
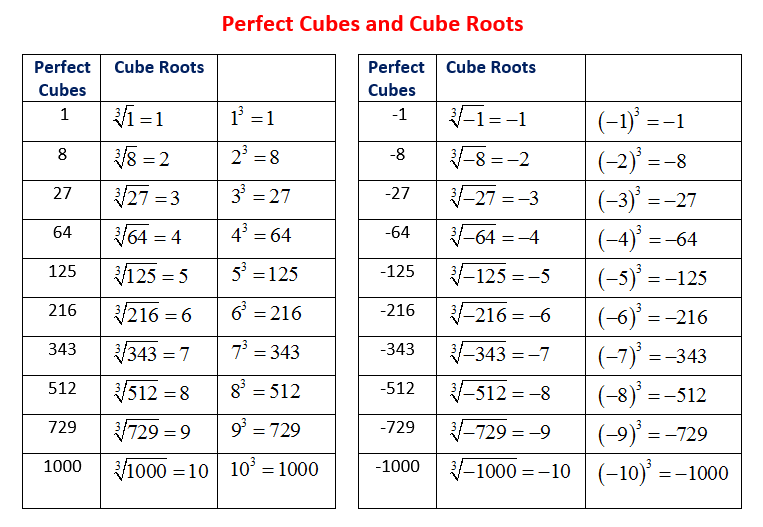
Perfect Cubes & Cube Roots
Evaluate Square Roots Of Perfect Squares And Cube Roots Of Perfect Cubes
How To Simplify Radicals With Negative Radicands And Odd Indexes?
Perfect Cubes And Cube Roots
To cube a number, we use the number in a multiplication 3 times.
For example, 4 cubed = 43 = 4 × 4 × 4 = 64
A cube root goes the other direction.
3 cubed is 27, so the cube root of 27 is 3.
The cube root of a number is the value that when cubed gives the original number.
The cube root of 27 is 3 because when 3 is cubed you get 27.
∛ is the special symbol that means “cube root”. It is the radical symbol √ with a little
three to mean cube root.
You can use it like this:
∛27 = 3.
Perfect cubes are cubes of whole numbers.
It is easy to work out the cube root of a perfect cube, but it is hard to work out other cube roots.
How To Find The Smallest Multiple Of Another Number That Is Also A Perfect Cube?
Example:
What is the smallest positive whole number that is a perfect cube and is a multiple of 24?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.