Graphs Of Reciprocal Functions

Related Pages
Reciprocal Of A Function
Graphs Of Functions

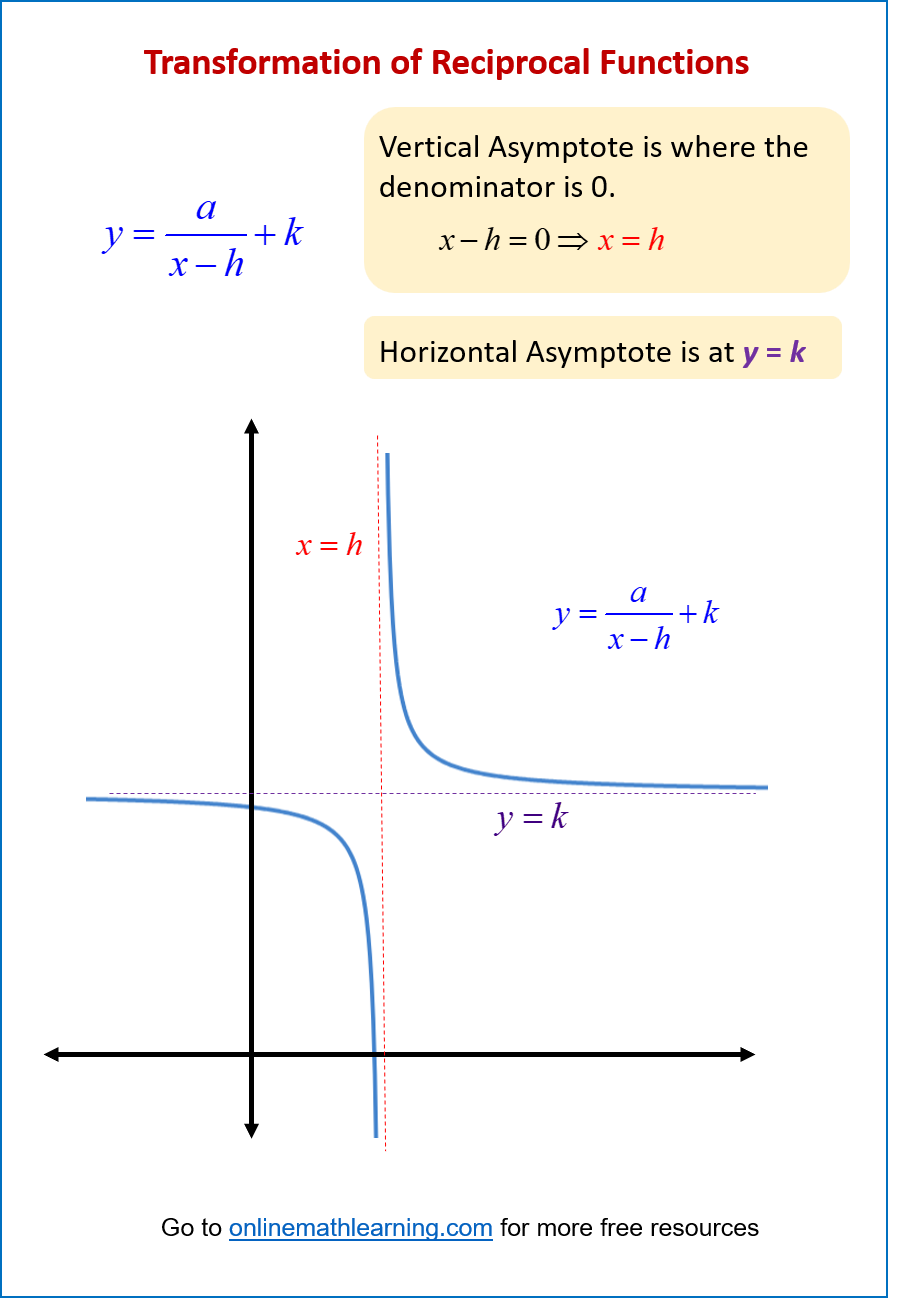
How To Graph Reciprocal Functions?

There are several forms of reciprocal functions. One of them has the form y = , where k is a real number and x ≠ 0.

What Are The Characteristics Of The Graph Of A Reciprocal Function?

The graph of y = gets closer to the x-axis as the value of x increases, but it never meets the x-axis. This is called the horizontal asymptote of the graph.

Each piece of the graph also gets closer to the y-axis as x gets closer to 0 but it never meets the y-axis because there is no value for y when x = 0. This is called the vertical asymptote of the graph.

This type of curve is called a rectangular hyperbola.

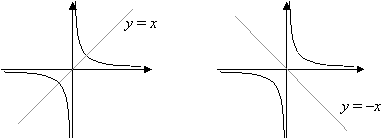
Note that this type of curve, the graphs of y = where k is a real number and x ≠ 0, has two lines of symmetry: y = x and y = x.

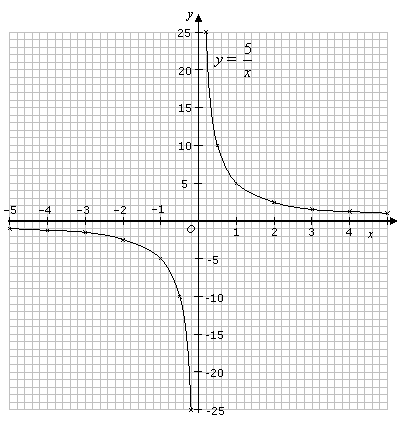
How To Graph Reciprocal Functions By Plotting Points?

Example:
Draw the graph of y = for values between 4 and 4, except for x = 0.

Solution:

x	0.2	0.5	1	2	3	4	5
y	25	10	5	2.5		1.25	1

x	0.2	0.5	1	2	3	4	5
y	25	10	5	2.5		1.25	1

The curve consists of two separate pieces, but they should be regarded as one graph.

How To Use Transformation To Graph Reciprocal Functions?

Introduction to reciprocal functions, identifying asymptotes and graphs of reciprocal functions, stretching, shrinking, and translating reciprocal functions, and graphing reciprocal functions.

y = 1/x and y = a/(x − h) + k.
Stretch when a > 1 and shrink when 0 < a < 1.
Graphs for positive and negative a values.
h translates horizontally and k translates vertically.

Examples:

1. Compare the graphs y = 1/x, y = 5/x and y = 1/(5x)
2. Compare the graphs y = 1/x and y = -1/x
3. Compare the graphs y = 1/x, y = 1/(x - 4) and y = 1/x - 4
4. Graph y = 2/(x - 4) + k

• Show Video Lesson

Describe The Characteristics Of The Reciprocal Function f(x) = 1/x

Explain the domain, range, vertical and horizontal asymptotes.

• Show Video Lesson

Transformation Of Reciprocal Functions

How to use transformation to graph reciprocal functions?

\(f(x) = \frac{a}{{x - h}} + k\)

h is the horizontal translation
if h is positive, shifts left
if h is negative, shifts right
h also shifts the vertical asymptote

k is the vertical translation
if k is positive, shifts up
if k is negative, shifts down
k also shifts the horizontal asymptote

a is orientation and shape
if a is negative, reflection across x-axis
if a > 1, stretched vertically
if 0 < a < 1, compressed vertically

Example:
Graph, then state the domain, range and asymptotes

1. \(f(x) = \frac{2}{{x}} + 3\)
   
2. \(f(x) = \frac{3}{{x - 2}}\)
   
3. \(f(x) = \frac{4}{{x + 3}} - 5\)
   
4. \(f(x) = \frac{4}{{x^2}} - 4\)
   
5. \(f(x) = 6 - \frac{2}{{(x - 3)^2}}\)

• Show Video Lesson

How To Graph A Reciprocal Function With A Horizontal Translation?

Sketch the Reciprocal Function using Transformations

Example:
Graph y = 1/(x - 3).

• Show Video Lesson

Graphing Transformations Of Reciprocal Function

Example:
Given the function \(y = \frac{{ - 2}}{{3(x - 4)}} + 1\)
a) Determine the parent function
b) State the argument
c) Rearrange the argument if necessary to determine and the values of k and d
d) Rearrange the function equation if necessary to determine the values of a and c
e) State the transformations (in an appropriate order) that are performed on the graph of the parent function to obtain the graph of the function given.

Method 1:
f) Graph each transformation in the appropriate order given in part e), and show the graph of the given function in a distinctive colour.

Method 2:
g) Use the table method to determine coordinate of the function given, the graph.

Method 3:
h) Use the transformation formula to determine coordinates of the function given, then graph.

• Show Video Lesson

How To Graph Reciprocal Functions When Given The Equation?

How to graph functions that are 1/x and variations of that.

Find asymptotes, intercepts, and use a couple test values.

1. To get the vertical asymptote, set denominator = 0
2. To get the horizontal asymptote, imagine x getting really big
3. To get the y-intercept, set x = 0
4. To get the x-intercept, set y = 0
5. Do test values on either side of the vertical asymptote

Example:
Graph m(x) = \(y = \frac{{ - 17}}{{18 - 8x}} - 4\).

• Show Video Lesson

How To Find The Equation Of A Reciprocal Function When Given Its Graph?

This video shows how to get the equation of a reciprocal function from its graph.

1. Find the vertical asymptote. This is the root of the denominator.
2. Find the horizontal asymptote. This is added/subtracted from your fraction.
3. Find a point on the curve, and plug into the equation. Solve for numerator.

• Show Video Lesson

Another form of reciprocal functions is y = , where k is a real number and x ≠ 0.

Example:
Draw the graph of y = for 4 ≤ x ≤4 and x ≠ 0.

Solution:

x	4	3	2	1	0.8	0.8	1	2	3	4
y	0.19	0.33	0.75	3	4.69	4.69	3	0.75	0.33	0.19

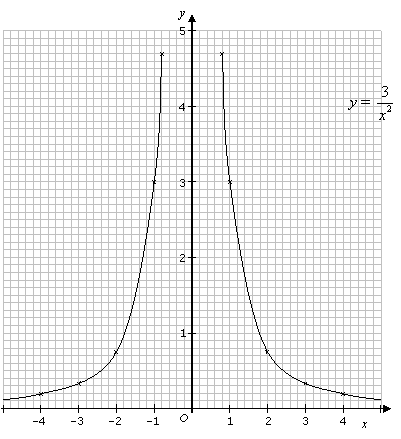
Notice that graphs of y = , where k is a real number and x ≠ 0, has an axis of symmetry on the y-axis (i.e. x = 0)

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.