Tangent Graphs
In these lessons, we will look at graphing the tangent function.
Related Pages
Trigonometric Graphs
Trigonometric Functions
Lessons On Trigonometry
We will start with the unit circle.
A unit circle is a circle of radius one unit with its center at the origin.
In the following diagram, the line l is a tangent to the unit circle at point P.
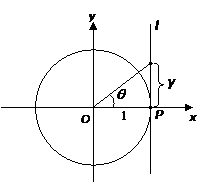
We can see that:
y = tan θ is known as the tangent function. Using the unit circle, we can plot the values of y against the corresponding values of θ.
The graph of y = tan θ, for 0˚ ≤ θ ≤ 360˚ obtained is as shown:
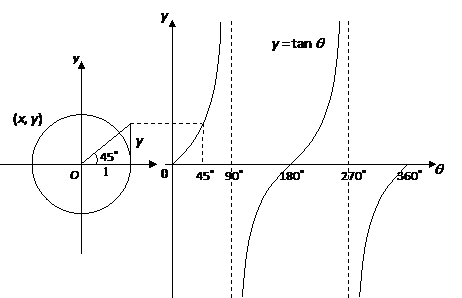
Properties of the tangent function:
- The curve is not continuous. It breaks at θ = 90˚ and 270˚, where the function is undefined
- tan θ = 0 when θ = 0˚, 180˚, 360˚. tan θ = 1 when θ = 45˚ and 225˚.
- tan θ = –1 when θ = 135˚ and 315˚.
- tan θ does not have any maximum or minimum values. The range of values of tan θ is –∞ < tan θ < ∞ .
- As the point P moves round the circle in either the clockwise or anticlockwise direction, the tangent curve above repeats itself for every interval of 180˚. Its period is 180˚.
Example:
Sketch the graph of y = tan x for 0˚ ≤ x ≤ 360˚.
Solution:
Set up a table of values for y = tan x
| x | 0 |
45 |
90 |
135 |
180 |
225 |
270 |
315 |
360 |
tan x |
0 |
1 |
undefined |
–1 |
0 |
1 |
undefined |
–1 |
0 |
Plot the points and join with a smooth curve.

Example:
The diagram shows a graph of y = tan x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r.
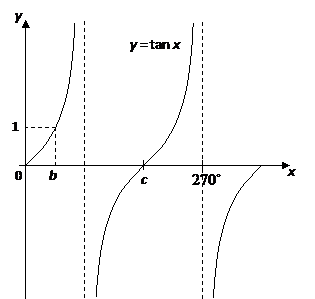
Solution:
We know that for a tangent graph, tan θ = 1 when θ = 45˚ and 225˚. So, b = 45˚.
We know that for a tangent graph, tan θ = 0 when θ = 0˚, 180˚ and 360˚. So, c = 180˚.
Graphing the Tangent Function
Demonstrates how to graph the tangent function using the unit circle.
Graphing the Tangent Function
How to graph the tangent function on the coordinate plane using the unit circle.
How to determine the domain and range of the tangent function.
The name of the tangent function comes from the tangent line that is perpendicular to the radius and intersects the circle at a single point.
To create a tangent segment, draw a line perpendicular to the x-axis and then extend θ so it intersects the tangent line. The tangent function is defined as the length of the red segment.
- The domain is {x|x ≠ (2n+1)(π/2)}, Range is (-∞, ∞)
- The graph is discontinuous and has vertical asymptotes.
- The x-intercepts occur at x = nπ
- The period is π
- The graph has no amplitude.
- The graph is symmetric with respect to the origin. Therefore, the function is an odd function.
Graph a Transformation of the Tangent Function (Period and Horizontal Shift)
y = A tan (B(x - D)) + C
- Tangent has no amplitude.
- π/B is the period.
- C is the vertical translation.
- D is the horizontal translation.
Example:
y = 3 tan (2x + π/2)
- Find the period of the function.
- Find the horizontal shift.
- Graph the function.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.