Transformation - Translation, Reflection, Rotation, Enlargement
Related Pages
Translation
Rotation
Transformations In Math
Transformations In The Coordinate Plane
More Geometry Lessons
These lessons help GCSE/IGCSE Maths students learn about different types of Transformation: Translation, Reflection, Rotation and Enlargement.
The following figures show the four types of transformations: Translation, Reflection, Rotation, and Enlargement. Scroll down the page for more examples and solutions using the transformations.
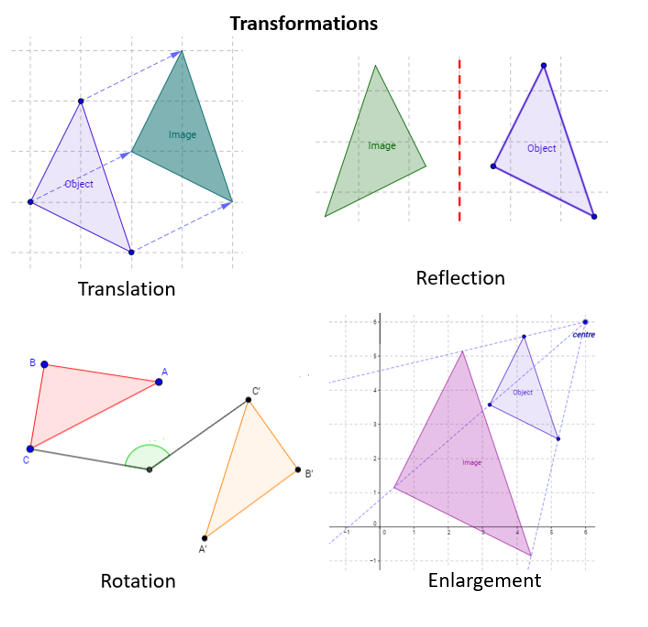
Translation
We translate a shape by moving it up or down or from side to side, but its appearance does not change in any other way. When we translate a shape, each of the vertices must be moved in exactly the same way. Every translation has a translation vector which gives the distance and direction in which the shape is moved.
How to translate a shape given the translation vector?
This video shows how to transform a shape using a given translation vector.
GCSE foundation maths transformations - Translating a shape
Examples:
- Plot the points (1,1), (2,1) and (1,2) and connect the dots to make a polygon.
Label your shape A and carry out the transformation. Translate A by the given vector and label the shape B. - State fully the single transformation that maps A to B.
Reflection
When we reflect a shape, we ‘flip’ it over a line of symmetry or ‘mirror’.
GCSE Maths transformations: Reflections in horizontal and vertical lines
Understand simply how to reflect shapes in vertical and horizontal lines. The trick is in understanding the equations of the horizontal and vertical lines. Reflections to help with GCSE mathematics, one in a line of the form x = a another in a line of the form y = b.
How to reflect on the coordinate plane?
Examples:
(a) Reflect shape A in the x-axis and label it shape B.
(b) Reflect shape A in the y-axis and label it shape C.
(c) Reflect shape A in the line x = 3 and label it shape D.
(d) Reflect shape A in the line y = 3 and label it shape E.
(e) Reflect shape A in the line y = -0.5 and label it shape F.
(f) Reflect shape A in the line y = x and label it shape G.
(g) Reflect shape A in the line y = -x and label it shape H.
Rotation
When we rotate a shape, we turn it a certain number of degrees around a fixed point. When describing a rotation, we need to describe the center of rotation, the angle of rotation and the direction of rotation.
GCSE transformation: Rotations about the origin
Transformations - Rotate 90 degrees
Rotating a polygon around the origin.
For a 90-degree rotation around the origin, switch the x,y values of each ordered pair for
the location of the new point.
How to rotate shapes with and without tracing paper?
Example:
Rotate ABC about (0,-1) by 90° clockwise.
Enlargement
When describing enlargement, we must state the scale factor and the centre of enlargement.
GCSE transformations: enlargement by positive and negative scale factor
GCSE mathematics revision help. An example on how to enlarge a shape by a positive and negative scale factor for GCSE revision. A scale factor of 2 and -2 is chosen.
Enlargement with Fractional and Negative Scale Factors
GCSE Maths revision Exam paper practice & help.
Example:
Triangle PQR is shown on the grid.
(a) Enlarge triangle PQR by scale factor 1/3 with centre of enlargement C(4,5)
(b) Triangle PQR is enlarged by scale factor -3 with centre of enlargement C(4,5).
P is mapped onto (31,14). Calculte the coordinated of the point that Q is mapped onto.
Translation, Reflection, Rotation And Enlargement
Three transformations from GCSE mathematics
Reflection, rotation and enlargement from GCSE mathematics, foundation level.
Examples:
(a) Enlarge triangle T by scale factor 3, centre the origin. Label the image A.
(b) Rotate the triangle T through 90° anti-clockwise anout the origin. Label the image B.
(c) Reflect triangle I in the line x = 4. Label the image C.
Describe the transformation and draw the image
GCSE Math AQA Q6 Higher Paper 1 June 2007
Example:
The diagram shows two triangles, A and B.
(a) Describe fully the single transformation that maps triangle A onto triangle B.
(b) On the diagram, draw an image of triangle after it is reflected in the line y = x. Label your image C.
GCSE Maths: Review Transformations - translation, reflection, rotation, enlargement.
Transformations: Translation and Enlargement D Grade.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.