Vector Magnitude

Related Pages
Vectors
Equal Vectors
Vector Multiplication
Vector Geometry

The length of a vector is called the magnitude or modulus of the vector.
The following diagram shows the magnitude of a vector. Scroll down the page for more examples and solutions to calculate the magnitude of 2-D and 3-D vectors .

Example:
Express each of the following vectors as a column vector and find its magnitude.

Vectors in 2D

Adding vectors geometrically, scalar multiplication, how to find the magnitude and direction angle of a vector.
A vector with initial point at the origin and terminal point at (a, b) is written <a, b>.
Geometrically, a vector is a directed line segment, while algebraically it is an ordered pair.

Example:
Find the magnitude and the direction angle for u = <-3, 4>

• Show Video Lesson

Vectors: magnitude of a vector in 2D.

Example:
Find the magnitude of the following vectors:
a = 4i - 3j
b = -2i + 5j

• Show Video Lesson

Vectors in 3D

The following diagram shows how to find the magnitude of a 3D Vector.

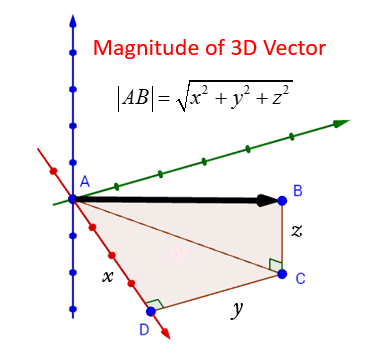
A vector can also be 3-dimensional.
The following video gives the formula, and some examples of finding the magnitude, or length, of a 3-dimensional vector.

Example:
Find the magnitude:
a = <3, 1, -2>
b = 5i -j + 2k

Vectors : Magnitude of a vector 3D.

Examples:

1. Find the magnitude of a = 4i + 3j + 2k
2. If A(3, -5, 6) and B(4, 1, 3) find the length AB.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.