Volume Formulas

In this lesson, we give

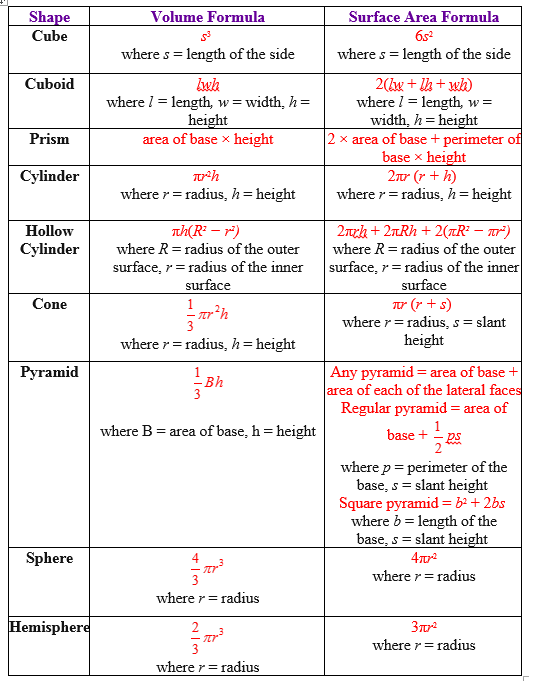
• a table of volume formulas and surface area formulas used to calculate the volume and surface area of three-dimensional geometrical shapes: cube, cuboid, prism, solid cylinder, hollow cylinder, cone, pyramid, sphere and hemisphere.
• a more detailed explanation (in text and video) of each volume formula.

Related Topics: More Geometry Lessons

Shape	Volume Formula	Surface Area Formula
Cube	s3 where s = length of the side	6s2 where s = length of the side
Cuboid	lwh where l = length, w = width, h = height	2(lw + lh + wh) where l = length, w = width, h = height
Prism	area of base × height	2 × area of base + perimeter of base × height
Cylinder	πr2h where r = radius, h = height	2πr (r + h) where r = radius, h = height
Hollow Cylinder	πh(R2 − r2) where R = radius of the outer surface, r = radius of the inner surface	2πrh + 2πRh + 2(πR2 − πr2) where R = radius of the outer surface, r = radius of the inner surface
Cone	where r = radius, h = height	πr (r + s) where r = radius, s = slant height
Pyramid		Any pyramid = area of base + area of each of the lateral faces Regular pyramid = area of base + ps where p = perimeter of the base, s = slant height Square pyramid = b2 + 2bs where b = length of the base, s = slant height
Sphere	where r = radius	4πr2 where r = radius
Hemisphere	where r = radius	3πr2 where r = radius

Cubes

A cube is a three-dimensional figure with six matching square sides.

The figure above shows a cube. The dotted lines indicate edges hidden from your view.

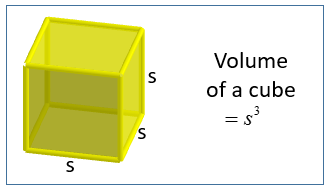
If s is the length of one of its sides, then the volume of the cube is s × s × s

Volume of the cube = s³

Worksheets to calculate volume and surface area of cubes
More examples about the volume of cubes
More examples about the surface area of cubes

How to find the volume of a cube?
The formula for the volume of a cube is s × s × s = s³, where s is the length of a side of the cube.

Rectangular Solids

A rectangular solid is also called a rectangular prism or a cuboid.

In a rectangular solid, the length, width and height may be of different lengths.

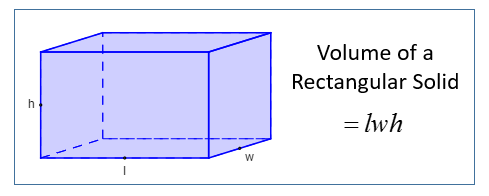
The volume of the above rectangular solid would be the product of the length, width and height that is

Volume of rectangular solid = lwh

Worksheets to calculate the volume and surface area of rectangular prisms.
More examples about the volume of cuboids.
More examples about the surface area of cuboids.

How to find the volume of a rectangular prism or cuboid?
The formula for the volume of a cuboid is l × w × h = lwh, where l is the length, w is the width and h is the height of the rectangular prism.. This video will give two examples of finding the volume of a rectangular prism

Volume of Prism

A prism is a solid that has two parallel faces which are congruent polygons at both ends. These faces form the bases of the prism. The other faces are in the shape of rectangles. They are called lateral faces.A prism is named after the shape of its base.

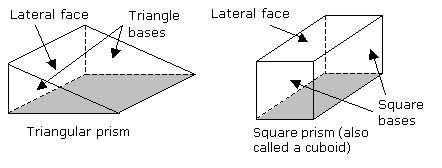
When we cut a prism parallel to the base, we get a cross section of a prism. The cross section has the same size and shape as the base.

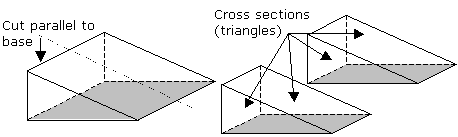
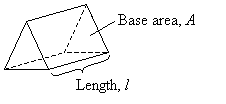
The volume of a right prism is given by the formula:
Volume of prism = Area of base × length

V = Al

where A is the area of the base and l is the length or height of the prism.

Worksheets to calculate volume of prisms and pyramids.
More examples about the volume of prisms.
More examples about the surface area of prisms.

How to find the volume of a triangular prism?
This video shows how to determine which is the base and the height of the triangular prism.

 

Volume of Cylinder

A cylinder is a solid that has two parallel faces which are congruent circles. These faces form the bases of the cylinder. The cylinder has one curved surface. The height of the cylinder is the perpendicular distance between the two bases.

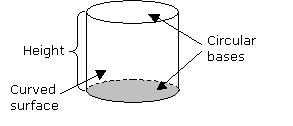
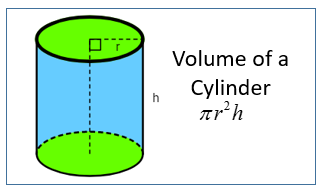
The volume of a cylinder is given by the formula:
Volume = Area of base × height

V = π r²h

where r = radius of cylinder and h is the height or length of cylinder.

Worksheets to calculate volume of cylinders.
Worksheets to calculate surface area of cylinders.
Worksheets to calculate volume and surface area of cylinders.
Worksheets to calculate surface area of cylinders and pipes.

More examples about the volume of cylinders.
More examples about the surface area of cylinders.

How to find the volume of a cylinder, given that the radius is 9 amd the height is 12.

Volume of hollow cylinder

Sometimes you may be required to calculate the volume of a hollow cylinder or tube.

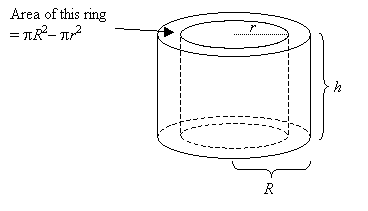
Volume of hollow cylinder

where R is the radius of the outer surface and r is the radius of the inner surface.

 

Volume of Cone

A cone is a solid with a circular base. It has a curved surface which tapers (i.e. decreases in size) to a vertex at the top. The height of the cone is the perpendicular distance from the base to the vertex.

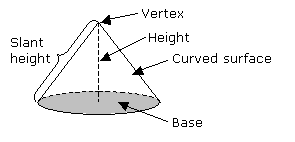
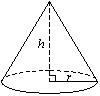
The volume of a cone is given by the formula:

Volume of cone = Area of base × height

V = where r is the radius of the base and h is the height of the prism.

Worksheets to calculate the volume of cones.
More examples about the volume of cones.
More examples about the surface area of cones.

How to find the volume of a cone, given that the radius is 12 and the height is 16?

 

Volume of Pyramid

A pyramid is a solid with a polygonal base and several triangular lateral faces. The lateral faces meet at a common vertex. The height of the pyramid is the perpendicular distance from the base to the vertex. The pyramid is named after the shape of its base. For example a rectangular pyramid or a triangular pyramid.

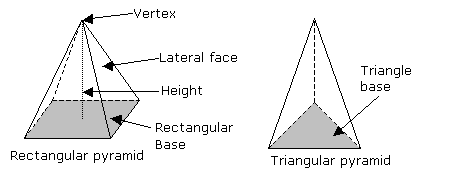
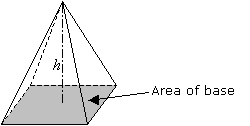
The volume of a pyramid is given by the formula:

Volume of pyramid = Area of base × height

V = where A is the area of the base and h is the height of the pyramid.

Worksheet to calculate the volume of square pyramids.
Worksheet to calculate the volume of prisms and pyramids.

More examples about the volume of pyramids.
More examples about the surface area of pyramids.

How to find the volume of a pyramid?
Make sure that you use the vertical height to substitute into the formula and not the slant height.

Volume of Sphere

A sphere is a solid in which all the points on the round surface are equidistant from a fixed point, known as the centre of the sphere. The distance from the centre to the surface is the radius.

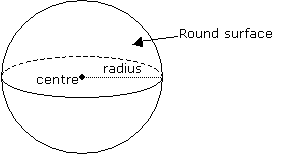
Volume of sphere = where r is the radius.

How to find the volume of a sphere? What is the volume of air in the ball?

 

Volume of a hemisphere

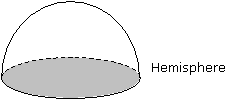
A hemisphere is half a sphere, with one flat circular face and one bowl-shaped face.

Volume of hemisphere where r is the radius

Worksheets to calculate the volume of spheres.
Worksheets to calculate the surface area of spheres.
More examples about the volume of spheres.
More examples about the surface area of spheres.

How to find the volume of a hemisphere? What is the volume of water in a bowl?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.