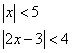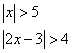Absolute Value Inequalities
More Lessons for Algebra
Math Worksheets
In this lesson, we will look into how to solve absolute value inequalities. Check out the lesson on what is meant by absolute value if necessary.
There are two types of absolute value inequalities, which are solved differently.
The “less than” type
For example:
The “greater than” Type
For example:
Let us first look at the “less than” type.
If the inequality looks like
then the solution looks like
– c < x < c
Example:
Solve ![]()
Solution:
–5 < x < 5
Example:
Solve ![]()
Solution:
–4 < 2x – 3 < 4
To isolate x, first add 3 to each term of the inequality
–1 < 2x < 7
then divide each term by 2
![]()
Now, we will look at the “greater than” type
If the inequality looks like
then the solution looks like
x < – c or x > c
Example:
Solve ![]()
Solution:
x < –5 or x > 5
Example:
Solve ![]()
Solution:
2x – 3 < –4 or 2x – 3 > 4
To isolate x, first add 3 to each term of the inequality
2x < –1 or 2x > 7
then divide each term by 2
![]()
Videos
Absolute Value Inequality ExampleSolve and graph the following inequality: |3x - 6| ≤ 12
Solve the absolute value inequality: |2x - 5| > 7
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.