Absolute Values

What is the absolute value of a number?
The absolute value of a number is the distance of the number from zero on the number line. The absolute value of a number is never negative. It is either positive or zero.

How to evaluate the absolute value of a number?

1. If the number is positive or zero: The absolute value is the number itself.
   Example: |6| = 6, |0| = 0
   
2. If the number is negative: The absolute value is the opposite (positive version) of that number.
   Example: |-4| = 4, |-12.5| = 12.5
   

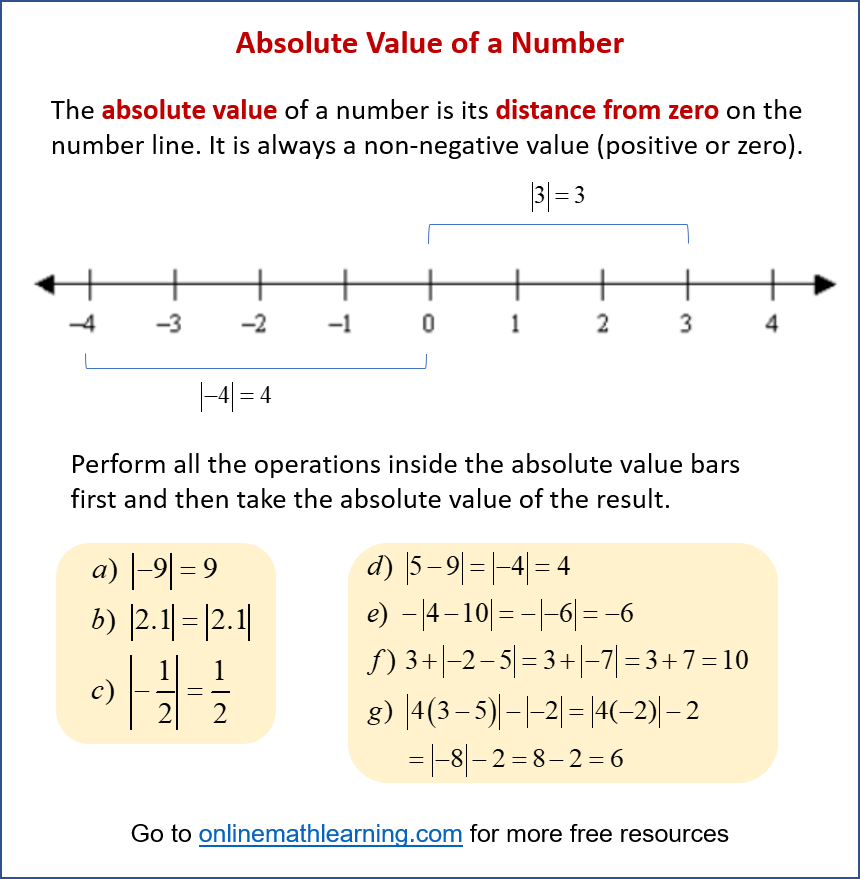
The following diagram shows what is the absolute value of a number and how to evaluate expressions with absolute values. Scroll down the page for more examples and solutions.

 

Absolute Value Worksheets
Practice your skills with the following worksheets:
Absolute Value Worksheets
Absolute Value Equation Worksheets

How to evaluate expressions with absolute values?
When you have expressions that include absolute values, you should first evaluate the expression inside the absolute value bars and then take the absolute value of the result. Example:
|5 - 8| = |-3| = 3
-|7 - 5| = -|2| = -2
-|4 - 8| = -|-4| = -4
7 + |-3 - 5| = 7 + |-8| = 7 + 8 = 15

Learn what an absolute value is, and how to evaluate it

This video explains absolute value in a way that actually makes sense. Using a number line, the concept of absolute value is illustrated through several example.

• Show Step-by-step Solutions

Math: Absolute Value

The absolute value bars act like a grouping symbol. Perform all the operations in the bar first and then change the sign to positive when necessary.
If there is a negative outside the absolute value bar, it stays there.
Work out the following examples.
Some examples of solving absolute value equations are also shown.
Examples:

1. Evaluate the following:
   |-5 + 4|
   -|2 - 3|
   -|6 + 1|
   |-8 + 9|
2. Solve for x
   |4 + x| = 8
   |-2 + x| = 4
   

• Show Step-by-step Solutions

Absolute Value and Evaluating Numbers
Absolute value makes things positive
The first step to simplifying absolute value problems is to simplify inside the absolute value, if possible.
Examples:
|5|
|-5|
|2 - 8|
|-2| - |10|
5|-3| + |-8|²
|3(4 - 8)| - |2(1 + 4)|²

• Show Step-by-step Solutions

Order of Operations - Absolute Value
The absolute value is like parenthesis. After simplifying what is in the bar, then we make the value positive.
Absolute value is like parenthesis. After evaluating inside then make positive at the end.
Examples:
-3|2⁴ - (5 + 4)²|
2 - 4|3² + (5² - 6²)|

• Show Step-by-step Solutions

How to solve Absolute Value Equations?
The absolute value of a number is its distance from zero on a number line.
The absolute-value principle for equations
For any positive number c and any algebraic expression x:

1. The solutions of |x| = c are those numbers that satisfy x = -c or x = c.
2. The equation |x| = 0 is equivalent to the equation x = 0.
3. The equation |x| = -c has no solution.

Check out the following lesson if you need a more detailed explanation:
Absolute Value Equations

How to solve an absolute value equation

1. Isolate the absolute value.
2. Set up and solve two equations based upon the absolute value principle.
   The solutions of |x| = c are those numbers that satisfy x = -c or x = c.
3. Check your answers.
   
   Examples: Solve the absolute value equations
4. |x| = 6
5. |x + 1| = -2
6. |2x + 3| -3 = 6
7. 2|4x - 2| + 4 = 12

How to solve absolute value equations graphically?

1. Graph the left side of the equation in y₁
2. Graph the right side of the equation in y₂
3. Determine the points of intersection. 4. The x-coordinates of the points of intersection are the solutions.
   Examples: Solve graphically
4. |x + 2| = 5
5. 3|-2x + 1| - 4 = 11

• Show Step-by-step Solutions

Examples of solving absolute value equations
Examples:
Solve
|x| = 4
|x + 4| = 12

• Show Step-by-step Solutions

Examples of solving absolute value equations
Examples:
Solve
|2x - 3| = 12
|1 - 3x| = -2

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.