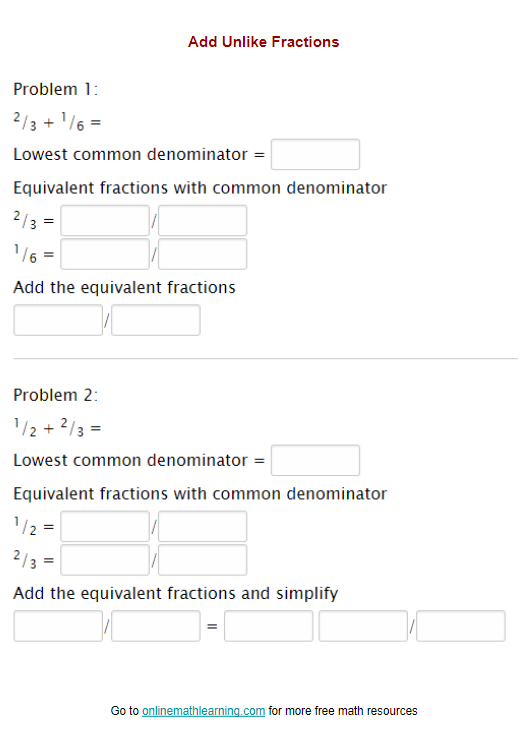
Add Unlike Fractions Worksheet

Printable “Add/Subtract Fractions” worksheets:
Add Like Fractions
Add Unlike Fractions
Subtract Like Fractions
Subtract Unlike Fractions
Subtract Fraction from Whole Number
Add/Subtract Fraction Word Problems

How to add unlike fractions?

Free printable and online worksheets to help Grade 5 students practice adding unlike fractions or fractions with unlike denominators. The fractions given are fractions with different denominators.

There are three printable worksheets. The first will provide some guidance on the steps to find the common denominator. The second will have sums that are proper fractions and reducing may be required. The third may have sums that are more than one and will require converting to mixed numbers.

There are some worksheets and fraction word problems for online practice followed by a shortcut method for adding fractions quickly.

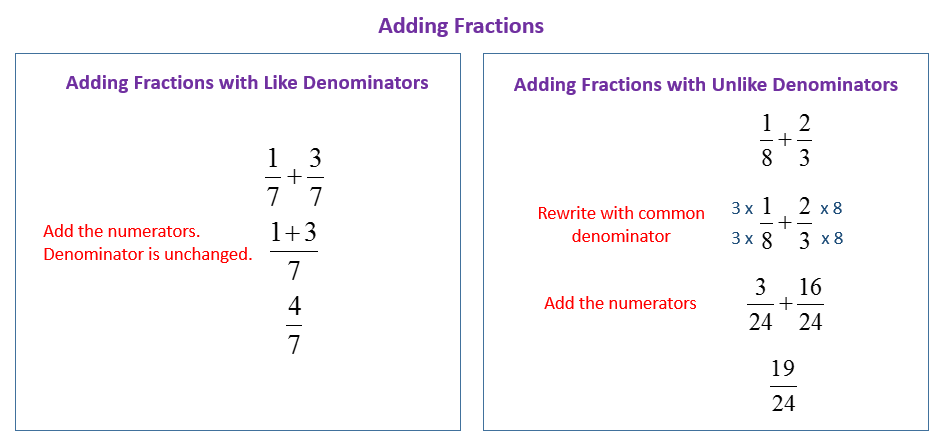
To add unlike fractions, you can follow these steps:
Step 1: Find a common denominator - the least common multiple (LCM) of the denominators of the fractions. This is the smallest number that both denominators can divide into evenly.
Step 2: Convert the fractions to equivalent fractions with the common denominator. To do this, multiply the numerator and denominator of each fraction by the necessary factor to make the denominator match the common denominator found in step 1.
Step 3: Add the numerators of the equivalent fractions obtained in step 2. The denominators remain the same.
Step 4: Simplify the resulting fraction, if possible, by finding the greatest common divisor (GCD) of the numerator and denominator, and dividing both by the GCD.

Here’s an example to illustrate the steps:

Example: Add 1/4 and 3/7
Step 1: Find a common denominator:
The multiples of 4 are: 4, 8, 12, 16, 20, …
The multiples of 7 are: 7, 14, 21, 28, …
The least common multiple (LCM) of 4 and 7 is 28. So, the common denominator is 28.
Step 2: Convert the fractions to equivalent fractions with the common denominator:
1/4 becomes 7/28 (multiplied numerator and denominator by 7)
3/7 becomes 12/28 (multiplied numerator and denominator by 4)
Step 3: Add the numerators of the equivalent fractions:
7/28 + 12/28 = 19/28
Step 4: Simplify the resulting fraction:
The fraction 19/28 is already simplified, as 19 and 28 do not share any common factors other than 1.
So, the sum of 1/4 and 3/7 is 19/28.

Example:

 

Have a look at this video if you need to review how to add fractions.

• Add Unlike Fractions

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Add Unlike Fractions Worksheets.

 

More Add Unlike Fractions Worksheets

Printable
(Answers on the second page.)
Add Unlike Fractions Worksheet #1 (step-by-step)
Add Unlike Fractions Worksheet #2 (sums are proper fractions)
Add Unlike Fractions Worksheet #3 (sums are mixed numbers)
Add Unlike Fractions Worksheet #4

Online
Add Like Fractions (no reducing)
Subtract Like Fractions (no reducing)
Add/Subtract Like Fractions

Least Common Denominator
Add/Subtract Unlike Fractions (step-by-step)
Add/Subtract Unlike Fractions

Adding Mixed Numbers

Add Unlike Fractions Word Problems

1. Jackie brought 3/4 of a gallon of iced tea to the party. Bill brought 7/8 of a gallon of iced tea to the same party. How much iced tea did Jackie and Bill bring to the party?
   • Show Answer

     13/8 = 1 5/8

2. On Monday, Ka practices guitar for 2/3 of one hour. When she’s finished, she practices piano for 3/4 of one hour. How much time did Ka spend practicing instruments on Monday?
   • Show Answer

     17/12 = 1 5/12

3. A recipe requires 3/4 pound of flour, and another recipe requires 1/3 pound of flour. How much flour is needed for both recipes?
   • Show Answer

     13/12 = 1 1/12

Shortcut to Adding Fractions

There is a shortcut to add unlike fractions.
Here’s how it works:
Step 1: Identify the unlike fractions you want to add. For example, let’s add 1/3 and 2/5.
Step 2: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.

1/3 + 2/5 [(1 × 5) + (2 × 3)] / (3 × 5)

Step 3: Add the results from step 2 in the numerator, and write the common denominator as the denominator.

(5 + 6) / 15

Step 4: Simplify the fraction, if necessary.

11/15

So, the sum of 1/3 and 2/5 is 11/15. This shortcut can be useful when when you want to quickly calculate the sum of unlike fractions.

Have a look at this video if you need to review how to add fractions the shortcut.

• Add Unlike Fractions using a shortcut

Related Lessons & Worksheets

Lesson on Adding Fractions

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.