Adding and Subtracting Integers using Zero Pairs

Adding and subtracting integers using zero pairs is a hands-on, visual method that helps to understand the concept of positive and negative numbers canceling each other out.

What is a Zero Pair?
A zero pair consists of one positive counter (representing +1) and one negative counter (representing -1). When you combine a positive one and a negative one, their sum is zero:

(+1) + (-1) = 0

Zero pairs don’t change the value of a set of counters because they essentially add nothing (zero).

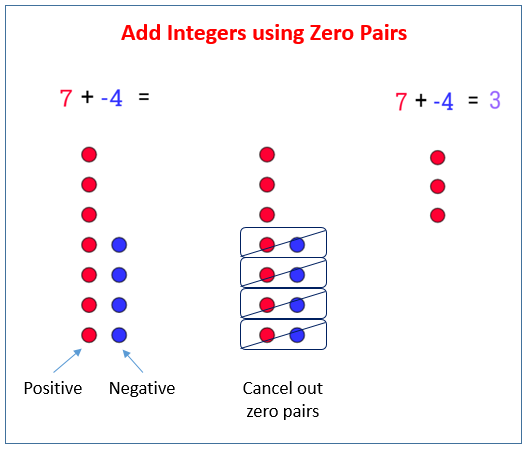
The following figure shows how to add integers using zero pairs. Scroll down the page for more examples and solutions.

 

Integer Worksheets
Practice your skills with the following integer worksheets:
Printable & Online Integer Worksheets

Using Zero Pairs for Addition:

1. Represent each integer using visual aids like colored counters. One color represents positive integers (e.g., blue), and another color represents negative integers (e.g., red).
2. Place the counters representing both integers together.
3. Look for pairs of one positive and one negative counter. Remove these pairs as they equal zero and don’t affect the final sum.
4. Count the remaining counters which represent the sum. The color indicates the sign (positive or negative), and the number of counters indicates the magnitude.

Using Zero Pairs for Subtraction:
Subtraction can be thought of as “taking away."
Case 1: You have enough counters to take away.
(Example: (+7)-(+2))

1. Place the number of counters indicated by the first integer.
2. Remove the number of counters indicated by the second integer.
3. Count the remaining counters: The remaining counters represent the difference.

Case 2: You don’t have enough counters to take away.
(Example: (+3)-(+5) or (+1)-(-4))
This is where zero pairs become crucial.

1. Place the number of counters indicated by the first integer.
2. Add an equal number of positive and negative counters (zero pairs) to your set. This doesn’t change the overall value. Add enough zero pairs so that you have enough of the counters you need to take away (the second integer).
3. Take away the second integer by removing the required number signed counters.
4. The remaining counters represent the difference.

Zero Pair Integers
Zero pairs are defined, discussed and utilized in the introductory video on zero pairs.
Example:
-4 + 6

• Show Step-by-step Solutions

How to add and subtract Integers?
Using integer dots to demonstrate the adding of integers using zero pairs.
The positive dots and negative dots cancel to leave the answer.
Examples:
6 + 2 =
-6 + (-2) =
6 + (-2) =
-6 + 2 =
-4 + -3 =
-2 + 5 =
-3 + 1 =
-2 + -2 =
-3 + 3 =

• Show Step-by-step Solutions

How to add Integers using the number line and zero pairs?
Examples:
-5 + 3
3 + (-6)
-2 + (-4)

• Show Step-by-step Solutions

Subtracting Integers by Adding Zero Pairs 3 - 2 =
2 - 6 =
1 - (-4) =

• Show Step-by-step Solutions

How to subtract positive and negative integers through the use of Red (negative) and Black (positive) tiles?
We introduce the concept of zero-pairs in this video lesson.
Example:
(-2) - 3

• Show Step-by-step Solutions

Understanding zero pairs
Zero pairs used in adding and subtracting integers
Examples:
3 + (-2)
3 - (-2)
5 - (-4)
-3 - 2

• Show Step-by-step Solutions

Learn how to add and subtract integers using integer tiles and zero pairs
Examples:
-5 + 3
-3 - 4
1 - 3

• Show Step-by-step Solutions

Why Zero Pairs Work:
Adding zero pairs is like adding zero to the problem. It doesn’t change the value of the initial integer, but it provides the necessary positive or negative counters to perform the subtraction.

Using zero pairs is a great way to build a concrete understanding of integer addition and subtraction before moving on to more abstract rules. It emphasizes the idea of opposites canceling each other out.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.