Adding and Subtracting Algebraic Expressions

Related Topics: More Algebra Lessons

In these lessons, we will learn how to simplify expressions by adding or subtracting like terms (combining like terms).

Simplifying Expressions Of Like Terms

An algebraic expression consisting of like terms can be simplified by adding or subtracting the coefficients of the like terms.

Example:

Simplifying the expressions:

a) 14x + 5x
b) 5y – 13y
c) p – 3p
d)

Solution:

a) 14x + 5x = (14 + 5)x = 19x
b) 5y – 13y = (5 –13)y = –8y
c) p – 3p = (1 – 3)p = – 2p
d)

Simplifying Expressions Of Like and Unlike Terms

To simplify an algebraic expression that consists of both like and unlike terms, we need to

Step 1: move the like terms together
Step 2: add or subtract their coefficients.

When moving the terms, we must remember to move the + or – attached in front of them. For example,

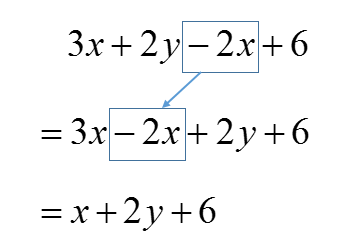
Example:

Simplify 3x + 2a – 4x

Solution:

3x + 2a – 4x
= 3x + 2a –4x
= 3x – 4x + 2a
= –x + 2a

Example:

Simplify b + 1.4c - 0.6b + 2

Solution:

b + 1.4c - 0.6b + 2
= b + 1.4c - 0.6b + 2
= b – 0.6b + 1.4c + 2
= 0.4 b + 1.4 c + 2

How to identify like terms and combine like terms?
Two or more like terms are like terms if they have the same variable (or variables) with the same exponent.
To combine like terms, we add or subtract the coefficients. The variable factors remain the same.
Examples:
Which of these terms are like terms?
-2x³, -2x, 2y, 7x³, 4y, 6x², y²
Simplify each polynomial, if possible.
4x³ - 7x³
2y² + 4y - y² + 2 - 9y - 5 + 2y

• Show Step-by-step Solutions

Identify and Combine Like Terms
Examples:
3v + 7v - v + v
5x + 6x² + 8x + x³ - x²
5c + 2d + c - (-3)d
1/2 y - 3/7 y + y

• Show Step-by-step Solutions

Examples of combining like terms
Examples:
1. 8x + 5y - 17x
2. 7x - 8 - 11x
3. 3a + 5c - 9a + 2a -c
4. 3xy + 4xy + 5x²y + 6xy²
5. 5y²x - 2x²y + 8y²x + 2xy - x²y + 3xy
6. 11a + 30a -18a

• Show Step-by-step Solutions

Simplify an Algebraic Expression by Combining Like Terms
This video shows how to simplify algebraic expressions by combining like terms by adding, subtracting, and using distribution.
Examples:
1. 4x³ + x² - 2x³ + 5
2. 10x⁵ + 3(2x⁵ - 4b²)

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.