AP Calculus AB 2008 Questions And Answers

AP Calculus AB is a college-level course and exam offered by the College Board. It covers the fundamentals of calculus, including limits, derivatives, integrals, and their applications. The course is equivalent to a first-semester college calculus course and is designed to prepare students for the AP Calculus AB exam, which can earn them college credit.

Questions And Worked Solutions For AP Calculus AB 2008

Click on the following image to get the complete paper of AP Calculus AB 2008 Free Response Questions. Scroll down the page for step-by-step solutions.

 
AP Calculus AB 2008 Free Response Questions - Complete Paper (pdf)

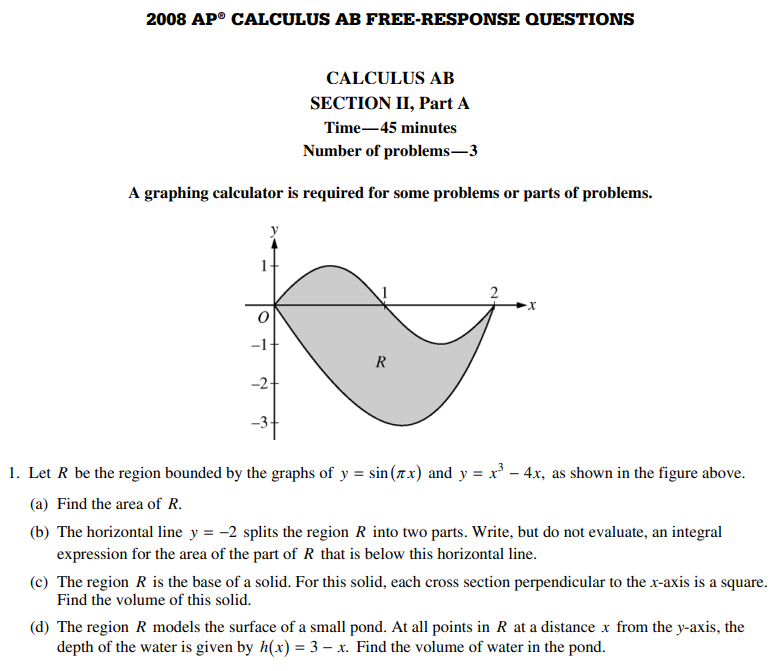
1. Let R be the region bounded by the graphs of y x = sin(πx) and y = x³ - 4x, as shown in the figure above.
   (a) Find the area of R.
   (b) The horizontal line y = −2 splits the region R into two parts. Write, but do not evaluate, an integral expression for the area of the part of R that is below this horizontal line.
   (c) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a square. Find the volume of this solid.
   (d) The region R models the surface of a small pond. At all points in R at a distance x from the y-axis, the depth of the water is given by h(x) = 3 - x . Find the volume of water in the pond.
2. Concert tickets went on sale at noon (t = 0) and were sold out within 9 hours. The number of people waiting in line to purchase tickets at time t is modeled by a twice-differentiable function L for 0 ≤ t ≤ 9.
   Values of L(t) at various times t are shown in the table above.
3. Oil is leaking from a pipeline on the surface of a lake and forms an oil slick whose volume increases at a constant rate of 2000 cubic centimeters per minute. The oil slick takes the form of a right circular cylinder with both its radius and height changing with time
4. A particle moves along the x-axis so that its velocity at time t, for 0 ≤ t ≤ 6 is given by a differentiable function v whose graph is shown above. The velocity is 0 at t = 0, t = 3, and t = 5, and the graph has horizontal tangents at t = 1 and t = 4. The areas of the regions bounded by the t-axis and the graph of v on the intervals [0,3], [3,5] and [5.6] are 8, 3, and 2, respectively. At time t 0, the particle is at x = -2.
5. Consider the differential equation
6. Let f be the function given by

Key Topics in AP Calculus AB:

1. Limits:
   Understanding the concept of a limit.
   Evaluating limits algebraically, graphically, and numerically.
   Continuity and the Intermediate Value Theorem.
   
2. Derivatives:
   Definition of the derivative as a limit.
   Rules of differentiation (power rule, product rule, quotient rule, chain rule).
   Derivatives of trigonometric, exponential, and logarithmic functions.
   
3. Applications of derivatives:
   Finding slopes of tangent lines.
   Related rates.
   Optimization.
   Linearization and differentials.
   Mean Value Theorem.
   Analysis of functions using the first and second derivatives.
   
4. Integrals:
   Definition of the definite integral as a limit of Riemann sums.
   The Fundamental Theorem of Calculus.
   Techniques of integration (u-substitution).
   
5. Applications of integrals:
   Finding areas under curves.
   Finding volumes of solids of revolution.
   Average value of a function.
   Differential equations and slope fields.
   

Exam Format:
The AP Calculus AB exam consists of two sections:
Section I: Multiple-Choice (50% of the exam grade)
Part A: No calculator.
Part B: Calculator allowed.
Section II: Free-Response (50% of the exam grade)
Calculator allowed for all free response questions.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.