AP Calculus BC 2023 Questions And Answers

AP Calculus AB is designed to be the equivalent of a first semester college calculus course devoted to topics in differential and integral calculus. AP Calculus BC is designed to be the equivalent to both first and second semester college calculus courses. AP Calculus BC applies the content and skills learned in AP Calculus AB to parametrically defined curves, polar curves, and vector-valued functions; develops additional integration techniques and applications; and introduces the topics of sequences and series.

Questions And Worked Solutions For AP Calculus BC 2023

Click on the following image to get the complete paper of AP Calculus BC 2023 Free Response Questions. Scroll down the page for step-by-step solutions.

 
AP Calculus BC 2023 Free Response Questions - Complete Paper (pdf)

• AP Calculus BC 2023 Free Response Question 1

• AP Calculus BC 2023 Free Response Question 2

• AP Calculus BC 2023 Free Response Question 3

• AP Calculus BC 2023 Free Response Question 4

• AP Calculus BC 2023 Free Response Question 5

• AP Calculus BC 2023 Free Response Question 6

1. A customer at a gas station is pumping gasoline into a gas tank. The rate of flow of gasoline is modeled by a differentiable function f, where f(t) is measured in gallons per second and t is measured in seconds since pumping began.
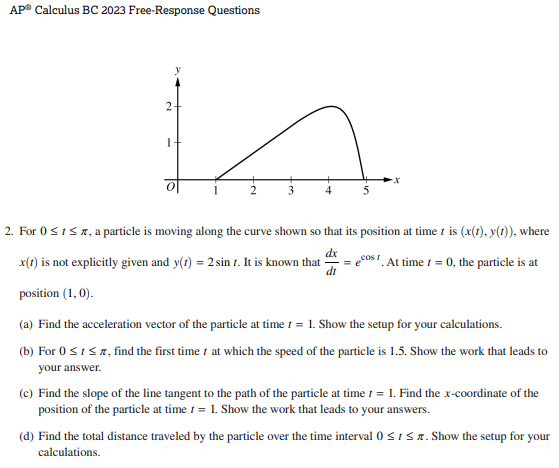
2. For 0 ≤ t ≤ π, a particle is moving along the curve agown so that its position at time t is (x(t), y(t)), where x(t) is not explicitly given and y(t) = 2 sin t.
3. A bottle of milk is taken out of a refrigerator and placed in a pan of hot water to be warmed. The increasing function M models the temperature of the milk at time t.
4. The function f is defined on the closed interval [-2,8] and satisfies f(2)=1. The graph of f’, the derivative of f, consists of two line segments and a semicircle, as shown in the figure.
5. The graphs of f and g are shown in the figure for 0 ≤ x ≤ 3.
6. The function f has derivatives of all orders for all real numbers. It is known that f(0) =2, f’(0) = 3, f’’(x) = -f(x²) and f’’’(x) = -2xf’(x²)

Key Topics Covered (Expands on AB):

1. All AP Calculus AB Topics:
   Limits and Continuity
   Derivatives (including all rules)
   Applications of Derivatives
   Integrals (including u-substitution)
   Fundamental Theorem of Calculus
   Applications of Integrals
   
2. Additional BC Topics:
   a) Advanced Integration Techniques:
   Integration by parts.
   Partial fractions.
   Improper integrals.
   b) Parametric Equations, Polar Coordinates, and Vector-Valued Functions:
   Derivatives and integrals of parametric equations.
   Derivatives and integrals in polar coordinates.
   Vector-valued functions and their derivatives and integrals.
   c) Infinite Series:
   Convergence and divergence of series.
   Taylor series and Maclaurin series.
   Power series.
   Lagrange error bound.
   d) Differential Equations:
   Euler’s method.
   Logistic differential equations.
   

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.