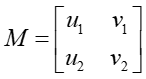Using Determinant to find the Area of a Parallelogram
Related Pages
Determinant of a 2×2 Matrix
Inverse of a 2×2 Matrix
Matrices
More Lessons for Grade 9
These lessons, with videos, examples and step-by-step solutions, help Algebra students learn how to use the determinant to find the area of a parallelogram. You can use the determinant of a matrix formed by the vectors representing the adjacent sides of a parallelogram to find its area.
Find Area Using Determinant
Determinants can be used to calculate the area of a parallelogram formed by 2 two-dimensional vectors. The matrix made from these two vectors has a determinant equal to the area of the parallelogram.
Area determinants are quick and easy to solve if you know how to solve a 2×2 determinant. A parallelogram in three dimensions is found using the cross product.
The following diagram shows how to find the area of a parallelogram formed by two vectors using determinant. Scroll down the page for more examples and solutions.
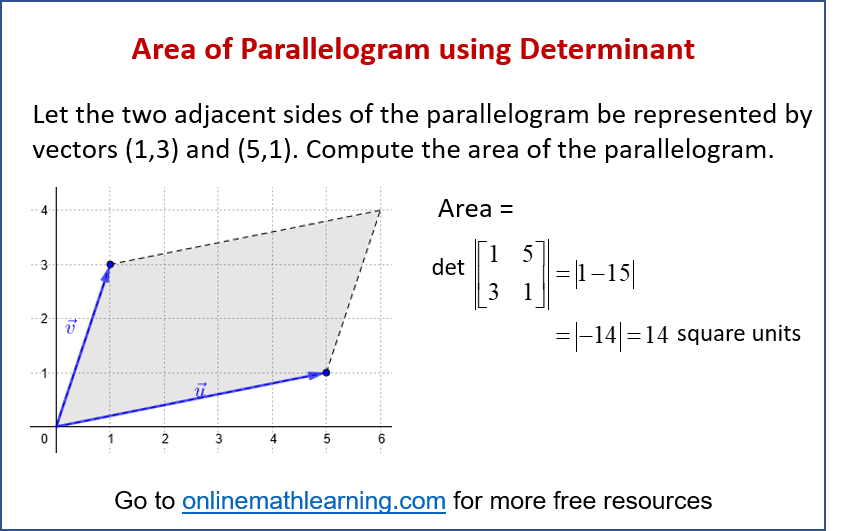
How to find the area of a parallelogram using determinant?
-
Represent the Sides as Vectors:
Let the two adjacent sides of the parallelogram be represented by vectors u = (u1, u2) and v = (v1, v2). -
Form a 2x2 Matrix:
Create a 2x2 matrix where the components of the vectors u and v form the rows (or columns) of the matrix.
If the parallelogram is represented by vectors u = (u1, u2) and v = (v1, v2) then form the matrix:
-
Calculate the Determinant:
The determinant of matrix M is: det(M) = (u1v2) - (u2v1) -
Find the Absolute Value:
The area of the parallelogram is the absolute value of the determinant calculated in the previous step.
Area = |det(M)| = (u1v2) - (u2v1)
Linear Algebra Example Problems - Area Of A Parallelogram
Also verify that the determinant approach to computing area yield the same answer obtained using “conventional” area computations.
Example:
Consider the parallelogram with vertices (0,0) (7,2) (5,9) (12,11)
Sketch and compute the area.
How to compute the area of a parallelogram using a determinant?
Determinant and area of a parallelogram
Realizing that the determinant of a 2x2 matrix is equal to the area of the parallelogram defined by the column vectors of the matrix.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.