Area of Rhombus
In this lesson, we will learn different formulas that can be used to calculate the area of a rhombus when we are
- given a side and height
- given lengths of the diagonals
- given a side and an angle
{#rhombus}Area of Rhombus
A rhombus has four equal sides and its diagonals bisect each other at right angles.
The following diagram shows how to find the area of a rhombus, given the lengths of the diagonals, or given the side and height, or given the side and an angle. Scroll down the page for more examples and solutions on finding the area of a rhombus.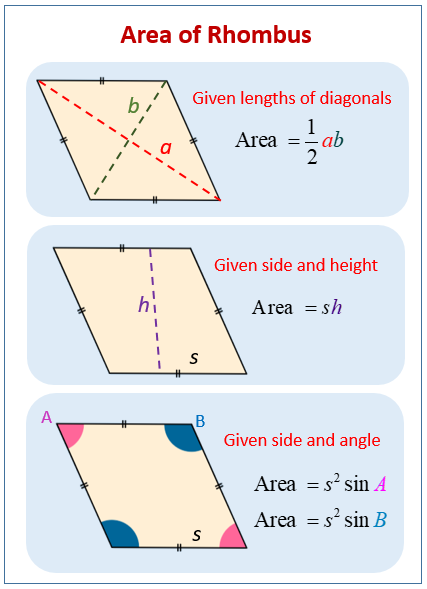 
Given Side and Height
If you are given the length of one side (s) and the perpendicular height (h) from one side to the vertex then the area of the rhombus is equal to the product of the side and height.
The area of the rhombus is given by the formula:
Area of rhombus = sh
This formula for the area of a rhombus is similar to the area formula for a parallelogram.
Given lengths of Diagonals
We can also obtain the area of a rhombus, given the lengths of its diagonals. The area of a rhombus is half the product of its diagonals.
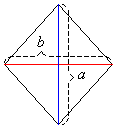
If the lengths of the diagonals are a and b, then area of the rhombus is given by the formula:
Area of rhombus =
How to calculate the area of a rhombus given the lengths of the diagonals?
How to proof that the area of a rhombus is equal to half the product of its diagonals?
Given a Side and an Angle
When given any side and any angle, the area of the rhombus is equal to product of the side squared and the sine of the angle.
Area of rhombus = s2 sin* a*
where s is the length of any side and a is any interior angle.
We can use any angle because either the angles are equal or they are supplementary, and supplementary angles have the same sine.
Problems using area of rhombus
The following video shows a problem involving the area of a rhombus.
The area of a rhombus is 16 cm2. If one diagonal has a length of 3 cm. Find the length of the other diagonal
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.