Calculus - Chain Rule
In these lessons, we look into how to use the chain rule to find the derivative of composite functions.
Related Pages
Calculus: Derivatives
Derivative Rules
Calculus: Power Rule
Calculus: Product Rule
Calculus Lessons
The Chain Rule
The following figure gives the Chain Rule that is used to find the derivative of composite functions. Scroll down the page for more examples and solutions.

In Leibniz notation, if y = f(u) and u = g(x) are both differentiable functions, then
![]()
Note: In the Chain Rule, we work from the outside to the inside. We differentiate the outer function and then we multiply with the derivative of the inner function.
Example:
Find the derivatives of each of the following

Solution:

Example:
Differentiate y = (2x + 1)5(x3 – x +1)4
Solution:
In this example, we use the Product Rule before using the Chain Rule.
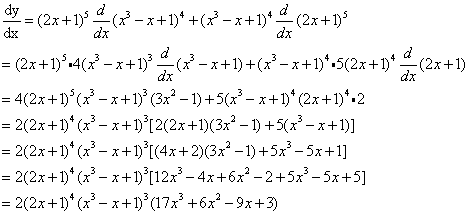
Chain Rule: The General Power Rule
The general power rule is a special case of the chain rule. It is useful when finding the derivative of a function that is raised to the nth power. The general power rule states that this derivative is n times the function raised to the (n-1)th power times the derivative of the function.
This tutorial presents the chain rule and a specialized version called the generalized power rule.
Several examples are demonstrated.
Errata: at (9:00) the question was changed from x2 to x4
Chain Rule: The General Exponential Rule
The exponential rule is a special case of the chain rule. It is useful when finding the derivative of e raised to the power of a function. The exponential rule states that this derivative is e to the power of the function times the derivative of the function.
Derivatives of Exponential Functions. Just some examples of finding derivatives of functions involving exponentials.
Chain Rule: The General Logarithm Rule
The logarithm rule is a special case of the chain rule. It is useful when finding the derivative of the natural logarithm of a function. The logarithm rule states that this derivative is 1 divided by the function times the derivative of the function.
Examples using the Chain Rule
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.