Circle Theorem for Arcs and Chords
Related Topics:
More Lessons for High School Regents Exam
Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
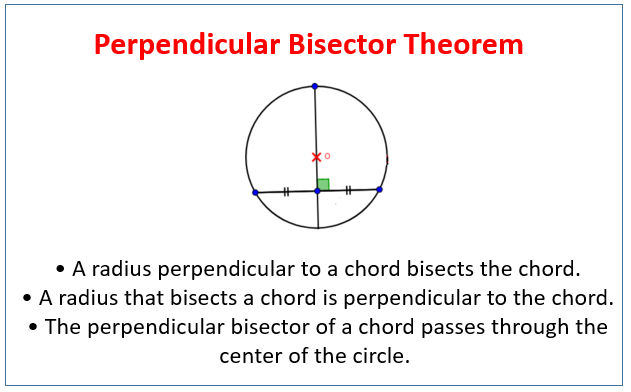
Theorem on Circles and Chords
In a circle, a radius perpendicular to a chord bisects the chord.
In a circle, a radius that bisects a chord is perpendicular to the chord.
In a circle, the perpendicular bisector of a chord passes through the center of the circle.
The following diagram gives the perpendicular bisector theorem for the chords in a circle. Scroll down the page for more examples and solutions.
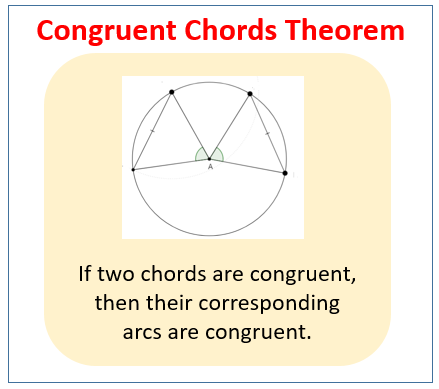
Theorem on Congruent Chords
In a circle, or congruent circles, congruent chords have congruent arcs. (converse) In a circle, or congruent circles, congruent arcs have congruent chords.
The following diagram gives the theorem for congruent chords. Scroll down the page for more examples and solutions.
Arcs and Chords
Radius drawn perpendicular to a chord bisects the chord and the arc
Circles: Arcs and Chords Pt 1
In a circle, or congruent circles, congruent chords have congruent arcs. (converse) In a circle, or congruent circles, congruent arcs have congruent chords. A diameter that is perpendicular to a chord bisects the chord and its arc
Circles: Arcs and Chords Pt 2
In a circle, or congruent circles, congruent chords have congruent arcs. (converse) In a circle, or congruent circles, congruent arcs have congruent chords. A diameter that is perpendicular to a chord bisects the chord and its arc
Circles: Arcs and Chords Pt 3
In a circle, or congruent circles, congruent chords have congruent arcs. (converse) In a circle, or congruent circles, congruent arcs have congruent chords. A diameter that is perpendicular to a chord bisects the chord and its arc
Arcs and Chords
If a diameter is perpendicular to a chord, then it bisects the chord and its arc.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.