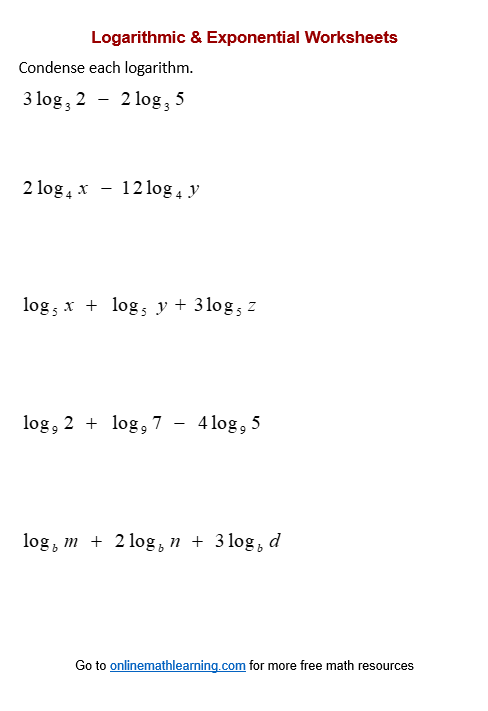Condense Logarithms Worksheets

There are four sets of logarithm & exponential worksheets:

• Exponential & Logarithmic Forms
  
• Evaluate Logarithms
  
• Expand Logarithms
  
• Condense Logarithms
  

Examples, solutions, videos, and worksheets to help Grade 7 and Grade 8 students learn how to condense logarithms.

How to condense logarithms?

There are two sets of condensing logarithm worksheets.

• Condense Logarithms.
• Condense Logarithms (Include Radicals).

Condensing logarithms means combining multiple logarithmic terms into a single, simplified logarithmic expression. Here are some techniques for condensing logarithms:

1. Product Rule for Logarithms:
   The product rule for logarithms states that
   log_b(M) + log_b(N) = log_b(MN).
   This rule allows you to combine two separate logarithmic terms that are being added into a single logarithmic term.
   For example, to condense log₂(5) + log₂(x):
   log₂(5) + log₂(x) = log₂(5x)

2. Quotient Rule for Logarithms:
   The quotient rule for logarithms states that
   log_b(M) - log_b(N) = log_b(M/N)
   This rule allows you to combine two separate logarithmic terms that are being subtracted into a single logarithmic term.
   For example, to condense log₅(8) - log₅(x)
   log₅(8) - log₅(x) = log₅(8/x)

3. Power Rule for Logarithms:
   The power rule for logarithms states that
   n log_b(M) = log_b(Mⁿ)
   This rule allows you to move the coefficient as an exponent inside the logarithm.
   For example, to condense 2 log₃(5)
   2 log₃(5) = log₃(5²)

These techniques can help you condense logarithmic expressions and simplify them into a more compact form. It’s essential to know when and how to use each method based on the specific logarithmic expression you’re working with.

Have a look at this video if you need to review how to condense logarithms.

• Condensing Logarithms

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Condense Logarithms Worksheets.

 

More Condense Logarithms Worksheets

Printable
(Answers on the second page.)
Condense Logarithms Worksheet #1
Condense Logarithms Worksheet #2 (Include Radicals)

Online
Apply Law of Exponents (multiply)
Apply Law of Exponents (mixed)

Related Lessons & Worksheets

Evaluate Logarithms by Expanding & Condensing

More Printable Worksheets

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.