Conditional Probability

Conditional probability is the probability of an event occurring given that another event has already occurred. It’s a fundamental concept in probability theory and statistics.

Notation:
The conditional probability of event A occurring given that event B has occurred is written as P(A|B).

The following diagram shows the formula for conditional probability. Scroll down the page for more examples and solutions on finding the conditional probability.

What Is Conditional Probability?

The probability of an event occurring given that another event has already occurred is called a conditional probability.

Recall that when two events, A and B, are dependent, the probability of both occurring is:

P(A and B) = P(A) × P(B given A)
or P(A and B) = P(A) × P(B | A)

If we divide both sides of the equation by P(A) we get the
Formula for Conditional Probability

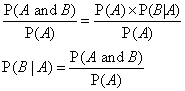
Intuitive Explanation:
Imagine you have a sample space of all possible outcomes. When you are given that event B has occurred, you are essentially restricting your focus to only the outcomes within event B. The conditional probability P(A|B) then asks, “Out of all the outcomes in event B, what proportion of them are also in event A?”

Steps to Calculate Conditional Probability:

1. Identify the events: Determine what event A is and what event B is.
2. Find P(A ∩ B): Calculate the probability of both A and B happening.
3. Find P(B): Calculate the probability of event B happening.
4. Apply the formula: Divide P(A ∩ B) by P(B).

How To Find The Conditional Probability From A Word Problem?

Step 1: Write out the Conditional Probability Formula in terms of the problem
Step 2: Substitute in the values and solve.

Example:
Susan took two tests. The probability of her passing both tests is 0.6. The probability of her passing the first test is 0.8. What is the probability of her passing the second test given that she has passed the first test?

Solution:

Example:
A bag contains red and blue marbles. Two marbles are drawn without replacement. The probability of selecting a red marble and then a blue marble is 0.28. The probability of selecting a red marble on the first draw is 0.5. What is the probability of selecting a blue marble on the second draw, given that the first marble drawn was red?

Solution:

Solution:
What is the probability that the total of two dice will be greater than 9, given that the first die is a 5?

Solution:
Let A = first die is 5
Let B = total of two dice is greater than 9

P(A) =

Possible outcomes for A and B: (5, 5), (5, 6)

P(A and B) =

 

How To Use Real World Examples To Explain Conditional Probability?

Conditional probability is about narrowing down the set of possible circumstances so that the statistics can be measured more accurately.

• Show Video Lesson

How To Define Conditional Probability?

This video introduces the basic definition of conditional probability as it is defined in standard probability theory.

• Show Video Lesson

How To Calculate Conditional Probability?

Tutorial on how to calculate conditional probability for two events P(A), P(B), P(B|A) with two examples.

• Example 1: What is the probability of rolling a dice and its value is less than 4 knowing that the value is an odd number?
• Example 2: What is the probability of rolling a dice and its value is 1 knowing that the value is an odd number?

• Show Video Lesson

How To Determine The Conditional Probability From The Given Word Problems?

Examples:

1. You roll one 6-sided die, what is the probability of a 3 given you know the number is odd?
2. At P-Town High School, the probability that a student takes Computer Programming and Spanish is 0.15. The probability that a student takes Computer Programming is 0.4.
   What is the probability that a student takes Spanish given that the student is taking Computer Programming?
3. Here are the results of a survey completed with adult parents with children. What is the probability a person thinks college is too expensive given they have a child in college?
4. Two cards are drawn without replacement in succession. What is the probability that the second card drawn is an ace, given that the first can drawn was an ace?
5. Two cards are drawn without replacement. What is the probability the second card is a red face card given the first card is a ref face card?

• Show Video Lesson

Relationship to Independence:
Two events A and B are independent if and only if:
P(A|B) = P(A)
P(B|A) = P(B)
P(A ∩ B) = P(A) * P(B)
If events are independent, the occurrence of one event does not affect the probability of the other event.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.