Cramer's Rule
Related Topics:
More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, games and activities to help Algebra students learn how to use Cramer’s Rule to solve a system of equations.
What is the Cramer’s Rule?
Cramer’s Rule is a method for solving systems of linear equations using determinants. It is particularly useful when you need to find the value of only one variable without solving the entire system.
The following diagram shows how to use Cramer’s rule to solve a systems of 3 equations. Scroll down the page for more examples and explanations on how to use the Cramer’s Rule.
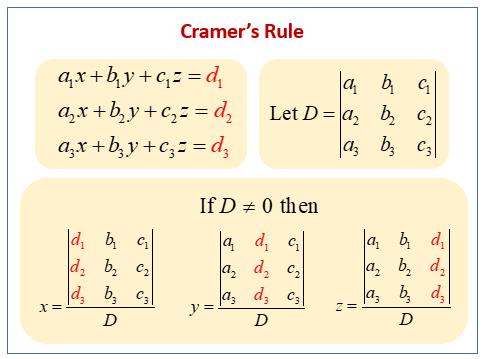
For a system of linear equations with the same number of equations as variables, we can find the value of each variable by taking the ratio of two determinants:
- The denominator is the determinant of the coefficient matrix (the matrix formed by the coefficients of the variables).
- The numerator is the determinant of a matrix formed by replacing the column corresponding to the variable you’re solving for with the constant terms from the equations.
Important: Cramer’s Rule only works if D ≠ 0. If D = 0, the system either has no solution or infinitely many solutions.
Cramer’s Rule
Sometimes using matrix algebra or inverse matrices to find the solution to a system of linear equations can be tedious. Sometimes it is more convenient to use Cramer’s Rule and determinants to solve a system of equations. Finding determinants becomes much more difficult with higher dimensions, and so Cramer’s Rule is better for smaller systems of linear equation.
Cramer’s rule, solving systems
How to use Cramer’s Rule to solve a system of equations?
Cramer’s Rule to Solve a System of 3 Linear Equations - Example 1
Cramer’s Rule to Solve a System of 3 Linear Equations - Example 2
Cramer’s rule, 3x3 linear system
How to solve a 3x3 system of linear equations using Cramer’s rule?
Advantages of Cramer’s Rule:
Provides a direct formula for finding the value of a specific variable.
Can be useful when you only need to find the value of one variable.
Disadvantages of Cramer’s Rule:
Can be computationally expensive for large systems of equations, as you need to calculate several determinants.
Does not work if the determinant of the coefficient matrix (D) is zero. In such cases, the system either has no solution or infinitely many solutions.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.