Cubes and Cube Root Worksheet

There are seven sets of exponents worksheets:

• Squares & cubes
  
• Squares & square roots
  
• Cubes & cube roots
  
• Whole number exponents
  
• Negative whole number exponents
  
• Unit fraction exponents (positive or negative)
  
• Fractional exponents (positive or negative)

Examples, solutions, videos, and worksheets to help Grade 6 and Grade 7 students learn how to find cubes and cube roots.

How to evaluate cubes and cube roots?

Cubes and cube roots are two closely related concepts in mathematics. A cube is a number that is multiplied by itself twice, and a cube root is a number that, when multiplied by itself twice, equals the original number. For example, 8 is a cube because it is equal to 2 multiplied by itself twice (2 × 2 × 2 = 8). The cube root of 8 is 2, because 2 × 2 × 2 = 8.

We can denote the cube of a number using exponents. For example, 2 × 2 × 2 = 3³ = 8.

The square root is denoted by the symbol “∛”. For example, the cube root of 8 is written as ∛9.
The cube of a negative number is negative, and the cube of a positive number is positive.
The cube root of a negative number is negative, and the cube root of a positive number is positive.

Perfect cubes are numbers that can be expressed as the square of an integer. It is obtained by multiplying an integer by itself twice. For example, 27 is a perfect cube because it can be expressed as 3 × 3 × 3 = 27. This also means that that the cube roots of perfect cubes are integers.

Other examples of cubes and cube roots:

 

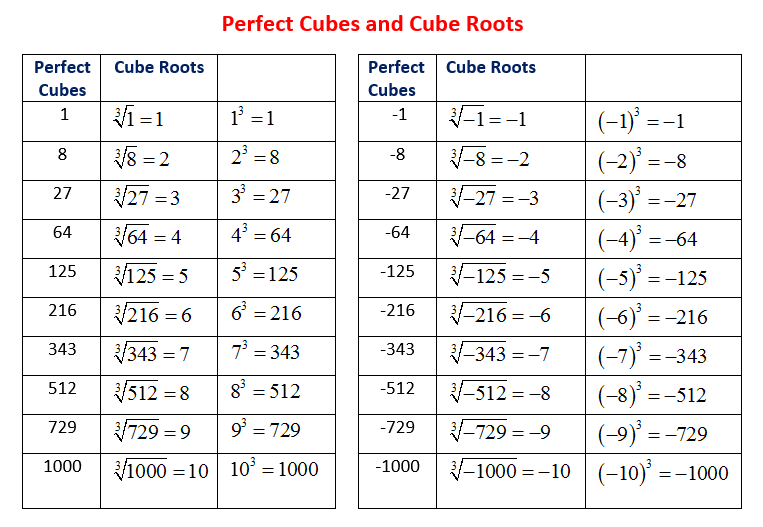
Have a look at this video if you need to review how to evaluate perfect cubes and cube roots.

• Perfect Cubes and Cube Roots

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Cubes and Cube Root Worksheets.

 

More Cubes and Cube Root Worksheets

Printable
(Answers on the second page.)
Cubes and Cube Root Worksheet

Generated
Squares with bases 0 to 10
Squares with bases 2 to 20
Squares with bases -10 to 0
Squares with bases -20 to 0

Cubes with bases 0 to 10
Cubes with bases 2 to 20
Cubes with bases -10 to 0
Cubes with bases -20 to 0

Related Lessons & Worksheets

Perfect Cubes

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.