Examples using the Derivative Rules

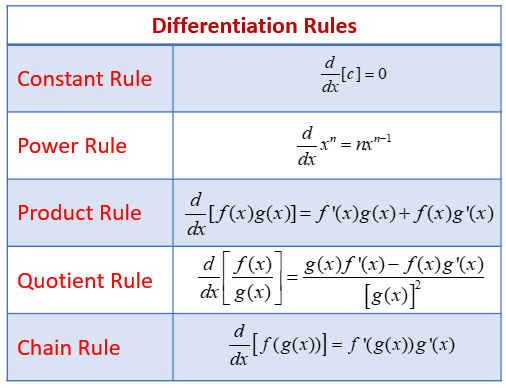
The following table shows the derivative or differentiation rules: Constant Rule, Power Rule, Product Rule, Quotient Rule, and Chain Rule. Scroll down the page for examples and solutions on how to use the rules.

 

Calculus Games/Worksheets
Practice your skills with the following worksheets:
Calculus Games and Worksheets

Examples to show how to use the different derivative rules.

Derivatives - Quotient and Chain Rule and Simplifying

• Show Step-by-step Solutions

Derivatives - Product + Chain Rule + Factoring

• Show Step-by-step Solutions

Product Rule, Chain Rule and Simplifying

• Show Step-by-step Solutions

Derivative Rules:
Basic Rules:

1. Constant Rule:
   If f(x) = c (where c is a constant), then f’(x) = 0.
   The derivative of a constant is always zero.
   
2. Power Rule:
   If f(x) = xⁿ (where n is any real number), then f’(x) = nx^(n-1).
   Bring down the exponent and subtract 1 from it.
   
3. Constant Multiple Rule:
   If f(x) = c * g(x) (where c is a constant), then f’(x) = c * g’(x).
   Constants multiply through the derivative.
   
4. Sum/Difference Rule:
   If f(x) = g(x) ± h(x), then f’(x) = g’(x) ± h’(x).
   The derivative of a sum or difference is the sum or difference of the derivatives.
   Product and Quotient Rules:
   
5. Product Rule:
   If f(x) = g(x) * h(x), then f’(x) = g’(x) * h(x) + g(x) * h’(x).
   “First derivative second plus second derivative first."
   
6. Quotient Rule:
   If f(x) = g(x) / h(x), then f’(x) = [g’(x) * h(x) - g(x) * h’(x)] / [h(x)]².
   “Low d-high minus high d-low over low squared."
   Chain Rule:
   
7. Chain Rule:
   If f(x) = g(h(x)), then f’(x) = g’(h(x)) * h’(x).
   “Derivative of the outside, leaving the inside alone, times the derivative of the inside."
   Trigonometric Derivatives:
   
8. Derivative of sin(x):
   d/dx [sin(x)] = cos(x)
   
9. Derivative of cos(x):
   d/dx [cos(x)] = -sin(x)
   
10. Derivative of tan(x):
    d/dx [tan(x)] = sec²(x)
    
11. Derivative of csc(x):
    d/dx [csc(x)] = -csc(x)cot(x)
    
12. Derivative of sec(x):
    d/dx [sec(x)] = sec(x)tan(x)
    
13. Derivative of cot(x):
    d/dx [cot(x)] = -csc²(x)
    Exponential and Logarithmic Derivatives:
    
14. Derivative of e^x:
    d/dx [e^x] = e^x
    
15. Derivative of ln(x):
    d/dx [ln(x)] = 1/x
    
16. Derivative of a^x:
    d/dx [a^x] = a^x * ln(a)
    

Important Notes:
The chain rule is particularly important and often used in conjunction with other rules.
Practice applying these rules to various functions to solidify your understanding.
These are the most used rules. There are of course inverse trig derivatives, and hyperbolic trig derivatives, etc.

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.