Direct Variation
Related Pages:
Proportions
Proportion Word Problems
Inverse Variation
Joint And Combined Variation
More Algebra Lessons
In these lessons, we will learn about direct variation and how to solve applications that involve direct variation.
Direct variation and inverse variation are two types of relationships between variables in mathematics. In this lesson, we will look at examples of direct variation word problems. Check out examples of inverse variation word problems in another lesson.
The following diagram shows the key differences between Direct Variation and Inverse Variation. Scroll down the page for examples and solutions.
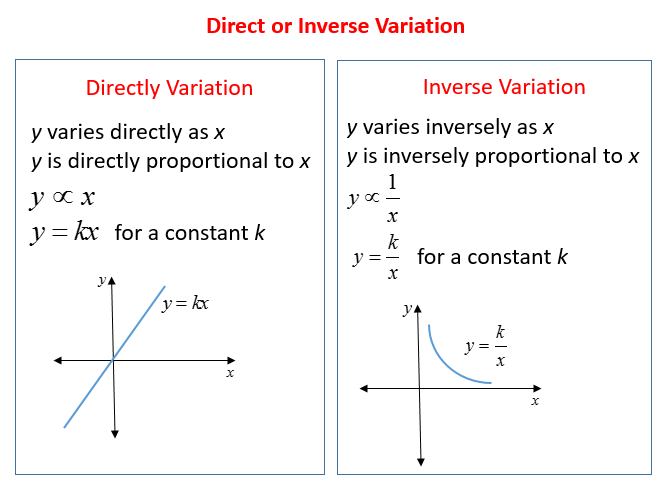
Variation Word Problems
Direct Variation Problems
Inverse Variation Problems
Joint & Combined Variations
What Is Direct Variation?
There are many situations in our daily lives that involve direct variation.
For example, a worker may be paid according to the number of hours he worked. The two quantities x (the number of hours worked) and y (the amount paid) are related in such a way that when x changes, y changes proportionately such that the ratio \(\frac{y}{x}\) remains a constant.
We say that y varies directly with x. Let us represent the constant by k, i.e.
\(\frac{y}{x} = k\) or y = kx where k ≠ 0
If y varies directly as x, this relation is written as y ∝ x and read as y varies as x. The sign “ ∝ ” is read “varies as” and is called the sign of variation.
General Steps to solve direct variation problems:
- Understand the Problem: Read the problem carefully. Identify the two quantities that are varying directly. Determine what information is given and what you need to find.
- Write the Basic Equation: Direct variation is represented by the equation y = kx, where:
y and x are the two quantities that vary directly.
k is the constant of variation (or constant of proportionality). This is the crucial value that relates the two quantities. - Find the Constant of Variation (k): The problem will give you a pair of values for x and y. Substitute these values into the equation y = kx and solve for k.
- Write the Specific Equation: Now that you know k, substitute its value back into the equation y = kx. This gives you the specific equation that relates the two quantities in this particular problem.
- Solve for the Unknown: The problem will ask you to find either x or y when given the other.
Example:
If y varies directly as x and given y = 9 when x = 5, find:
a) the equation connecting x and y
b) the value of y when x = 15
c) the value of x when y = 6
Solution:
a) y ∝ x i.e. y = kx where k is a constant
Substitute x = 5 and y = 9 into the equation:
\(9=5k\Rightarrow k=\frac{9}{5} \)
\(y=\frac{9}{5}x \)
b) Substitute x = 15 into the equation
\(y=\frac{9}{5}\times 15=27\)
c) Substitute y = 6 into the equation
\(6=\frac{9}{5}x\Rightarrow x=6\times \frac{5}{9}=\frac{10}{3} \)
Example:
The cost of a taxi fare (C) varies directly as the distance (D) travelled. When the distance is
60 km, the cost is $35. Find the cost when the distance is 95 km.
Solution:
C ∝ D i.e. C = kD, where k is a constant.
Substitute C = 35 and D = 60 into the equation
\(35=60k\Rightarrow k=\frac{35}{60}=\frac{7}{12} \)
Therefore, \(C = \frac{7}{12}D\)
Substitute D = 95 into the equation: C = \(\frac{7}{12} \times 95 = 55.42\)
The cost for 95 km is $55.42
How To Define Direct Variation And Solve Direct Variation Word Problems?
Some examples of direct variation problems in real life:
- The number of hours you work and the amount of your paycheck.
- The amount of weight on a spring and the distance the spring will stretch.
- The speed of a car and the distance traveled in a certain amount of time.
The following statements are equivalent:
- y varies directly as x
- y is directly proportional to x
- y = kx for some constant k
What Is The Direct Variation Formula?
A direct variation is a linear equation that can be written in the form y = kx , where k is a nonzero constant. The number k is called the constant of proportionality or constant of variation.
Graphically, we have a line that passes through the origin with the slope of k.
Examples:
- y varies directly with x. y = 54 when x = 9. Determine the direct variation equation and then determine y when x = 3.5
- Hooke’s Law states that the displacement, d, that a spring is stretched by a hanging object varies directly as the mass of the object. If the distance is 10 cm when the mass is kg, what is the distance when the mass is 5 kg?
- y varies directly with x. y = 32 when x = 4. Determine the direct variation equation and then determine y when x = 6
How To Determine A Direct Variation Equation From The Given Information And Then Determine y With A Given Value Of x?
Example: y varies directly with x. Given that y = 6 when x = 30, determine the direct variation equation and then determine y when x = 8.
Real Life Example Of A Direct Variation Problem
Example:
The total cost of filling up your car with gas varies directly with the number of gallons of
gasoline that you are purchasing. If a gallon of gas costs $2.25, how many gallons could you
purchase for $18?
Other Forms Of Direct Variation
The area A of a circle of radius r is given by the equation A = pr2, where p is a constant
In this situation, A is not directly proportional to r but A is directly proportional to r2. We say that ‘A varies directly as the square of r’ or A ∝ r2.
Example:
Given that y varies directly as the cube of x and that y = 21 when x = 3, calculate the value of y when x = 8.
Solution:
y ∝ x3 that is y = kx3 where k is a constant
Substitute x = 3 and y = 21 into the equation:
21 = k(33) ⇒ k = \(\frac{21}{27} = \frac{7}{9} \)
So, y = \(\frac{7}{9}\)x3
When x = 8, \(y=\frac{7}{9}(8)^3=\frac{3584}{9}=398\frac{2}{9} \)
The following video gives some practical examples of direct variation and indirect/inverse variation.
How To Solve Word Problems Involving Direct And Inverse Variation Squared?
Examples:
- On planet X, an object falls 18 feet in 2 seconds. Knowing that the distance it falls varies directly with the square of the time of the fall, how long does it take an object to fall 29 feet? Round your answer to three decimal places.
- The Intensity, I, of light received from a source varies inversely as the square of the distance, d, from the source. If the light intensity is 4-foot candles at 11 feet, find the light intensity at 13 feet.
Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.