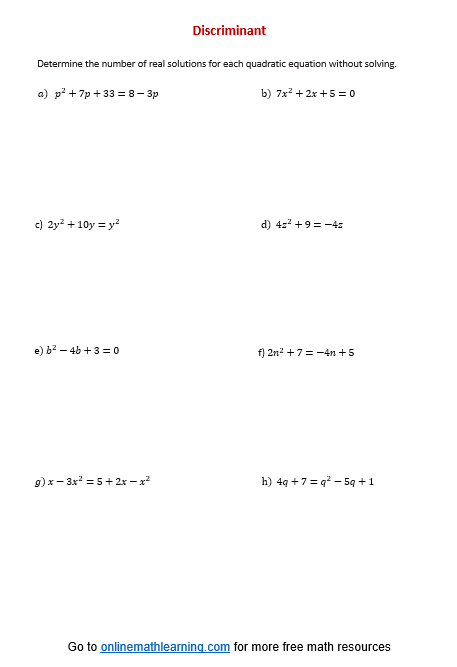Discriminant Worksheets

Printable “Quadratic Equations” worksheets:
Solve Quadratic Equation (use factoring)
Solve Word Problems using Quadratic Equations
Sketching Quadratic Graphs

Rewrite Expressions in Completed-Squared Form
Solve Quadratic Equation (use completing the square)
Solve Quadratic Equation (use quadratic formula)
Discriminant in the Quadratic Formula

Examples, solutions, videos, and worksheets to help Algebra1 students understand that the discriminant in the quadratic formula, b²-4ac, can be used to determine whether a quadratic equation has one, two, or no real solutions.

How to use the discriminant in the Discriminant?

The discriminant, b² - 4ac, is the part of the Discriminant that lies under the radical sign. It tells us about the nature of the roots of a quadratic equation of the form ax² + bx + c = 0.

For a quadratic equation in the standard form:

ax² + bx + c = 0

the discriminant 𝐷 is given by the expression under the square root in the Discriminant:
𝐷 = b² - 4ac

If the discriminant is positive (b² - 4ac > 0):
The quadratic equation has two distinct real roots.
The graph of the quadratic function intersects the x-axis at two distinct points.

If the discriminant is zero (b² - 4ac = 0):
The quadratic equation has one real root (a repeated root).
The graph of the quadratic function touches the x-axis at exactly one point.

If the discriminant is negative (b² - 4ac < 0):
The quadratic equation has no real roots. It has two imaginary roots.
The graph of the quadratic function does not intersect the x-axis.

Have a look at this video if you need to review how to use the discriminant.

• Discriminant in the Quadratic Formula

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Discriminant Worksheets.

 

More Discriminant Worksheets

Printable
(Answers on the second page.)
Discriminant Worksheet #1 (calculate discriminant)
Discriminant Worksheet #2 (include graphs)
Discriminant Worksheet #3 (include graphs)

Related Lessons & Worksheets

Quadratic Formula & Discriminant

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.