Illustrative Mathematics Unit 6.6, Lesson 11: The Distributive Property, Part 3

Related Pages
Illustrative Math
Grade 6

Lesson 11: The Distributive Property, Part 3

Let’s practice writing equivalent expressions by using the distributive property.

Illustrative Math Unit 6.6, Lesson 11 (printable worksheets)

Lesson 11 Summary

The following diagram shows how to use the distributive property to write equivalent expressions with variables.

Lesson 11.1 The Shaded Region

A rectangle with dimensions 6 cm and w cm is partitioned into two smaller rectangles.
Explain why each of these expressions represents the area, in cm², of the shaded portion.

• 6w - 24
• 6(w - 4)

• See Video for Whole Lesson

Scroll down the page for the solutions to the “Are you ready for more?” section.

Lesson 11.2 Matching to Practice Distributive Property

Match each expression in Column 1 to an equivalent expression in Column 2. If you get stuck, consider drawing a diagram.
Column 1
A. a(1 + 2 + 3)
B. 2(12 - 4)
C. 12a + 3b
D. 2/3(15a - 18)
E. 6a + 10b
F. 0.4(5 - 2.5a)
G. 2a + 3a
Column 2

1. 3(4a + b)
   
2. 12 · 2 - 4 · 2
   
3. 2(3a + 5b)
   
4. (2 + 3)a
   
5. a + 2a + 3a
   
6. 10a - 12
   
7. 2 - a
   

Lesson 11.3 Writing Equivalent Expressions Using the Distributive Property

The distributive property can be used to write equivalent expressions. In each row, use the distributive property to write an equivalent expression. If you get stuck, draw a diagram.

product	sum or difference
3(3 + x)
	4x - 20
(9 - 5)x
	4x + 7x
3(2x + 1)
	10x - 5
	x + 2x + 3x
1/2 (x - 6)
y(3x + 4z)
	2xyz - 3yz + 4xz

Are you ready for more?

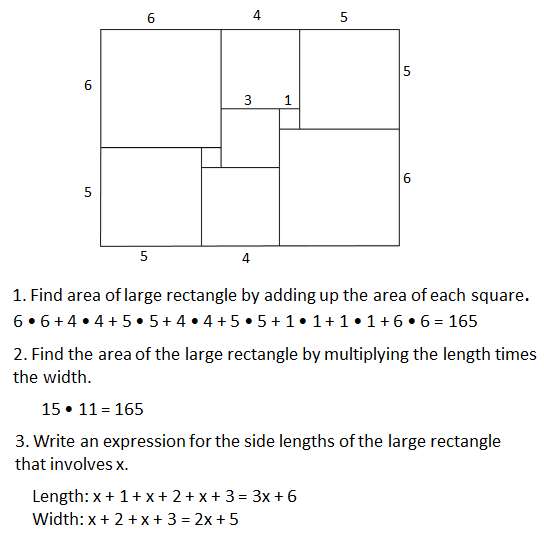
This rectangle has been cut up into squares of varying sizes. Both small squares have side length 1 unit. The square in the middle has side length x units.

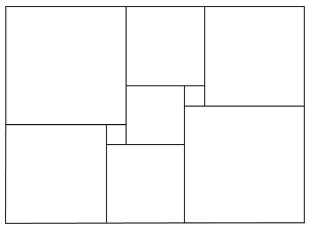
1. Suppose that x is 3. Find the area of each square in the diagram. Then find the area of the large rectangle.
2. Find the side lengths of the large rectangle assuming that x is 3. Find the area of the large rectangle by multiplying the length times the width. Check that this is the same area you found before.
3. Now suppose that we do not know the value of x. Write an expression for the side lengths of the large rectangle that involves x.
   • Show Answer

     

Lesson 11 Practice Problems

1. For each expression, use the distributive property to write an equivalent expression.
   a. 4(x + 2)
   b. (6 + 8) · x
   c. 4(3x + 3)
   d. 6(x + y + z)
   
2. Priya rewrites the expression 8y - 24 as 8(y - 3). Han rewrites 8y - 24 as 2(4y - 12). Are Priya’s and Han’s expressions each equivalent to 8y - 24? Explain your reasoning.
3. Select all the expressions that are equivalent to 16x + 36.
   A. 16(x + 20)
   B. x(16 + 36)
   C. 4(4x + 9)
   D. 2(8x + 18)
   E. 2(8x + 36)
   
4. The area of a rectangle is 30 + 12x. List at least 3 possibilities for the length and width of the rectangle.
5. Select all the expressions that are equivalent to 1/2 z.
   A. z + z
   B. z ÷ 2
   C. z · z
   D. 1/4 z + 1/4 z
   E. 2z
   
6. a. What is the perimeter of a square with side length:
   3cm, 7cm, scm
   b. If the perimeter of a square is 360 cm, what is its side length?
   c. What is the area of a square with side length:
   3cm, 7cm, scm
   d. If the area of a square is 121 cm², what is its side length?
   
7. Solve each equation.
   a. 10 = 4y
   b. 5y = 17.5
   c. 1.036 = 10y
   d. 0.6y = 1.8
   e. 15 = 0.1y
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.