Edexcel Core Mathematics C12 January 2015 Part 2
Questions and Worked Solutions for C12 Edexcel Core Mathematics January 2015, Part 2.
Related Pages
Edexcel C34 January 2015
More A Levels Past Papers
Download Edexcel Core Mathematics C12 January 2015 Past Paper (PDF)
Core 12 Mathematics Edexcel January 2015 Question 9
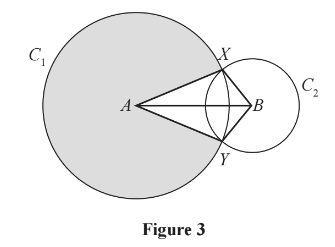
In Figure 3, the points A and B are the centres of the circles C1 and C2 respectively. The circle C1 has radius 10 cm and the circle C2 has radius 5 cm. The circles intersect at the points X and Y, as shown in the figure.
Given that the distance between the centres of the circles is 12 cm,
(a) calculate the size of the acute angle XAB, giving your answer in radians to 3 significant figures,
(b) find the area of the major sector of circle C1, shown shaded in Figure 3,
(c) find the area of the kite AYBX.
Core 12 Mathematics Edexcel January 2015 Question 10
f(x) = 6x3 + ax2 + bx - 5
where a and b are constants.
When f(x) is divided by (x + 1) there is no remainder.
When f(x) is divided by (2x – 1) the remainder is –15
(a) Find the value of a and the value of b.
(b) Factorise f(x) completely.
Core 12 Mathematics Edexcel January 2015 Question 11
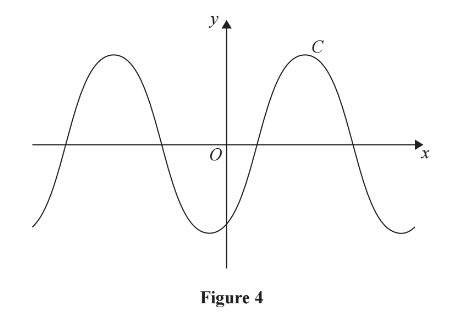
Figure 4 shows a sketch of the curve C with equation y = sin(x – 60°), –360° ≤ x ≤ 360°.
(a) Write down the exact coordinates of the points at which C meets the two coordinate axes.
(b) Solve, for –360° ≤ x ≤ 360°,
4 sin(x – 60°) = √6 - √2
showing each stage of your working.
Core 12 Mathematics Edexcel January 2015 Question 12
A business is expected to have a yearly profit of £275 000 for the year 2016. The profit is expected to increase by 10% per year, so that the expected yearly profits form a geometric sequence with common ratio 1.1
(a) Show that the difference between the expected profit for the year 2020 and the expected profit for the year 2021 is £40 300 to the nearest hundred pounds.
(b) Find the first year for which the expected yearly profit is more than one million pounds.
(c) Find the total expected profits for the years 2016 to 2026 inclusive, giving your answer to the nearest hundred pounds.
Core 12 Mathematics Edexcel January 2015 Question 13
The curve C has equation
y = 3x2 – 4x + 2
The line l1 is the normal to the curve C at the point P(1, 1)
(a) Show that l1 has equation
x + 2y – 3 = 0
The line l1 meets curve C again at the point Q.
(b) By solving simultaneous equations, determine the coordinates of the point Q.
Another line l2 has equation kx + 2y – 3 = 0, where k is a constant.
(c) Show that the line l2 meets the curve C once only when
k2 – 16k + 40 = 0
(d) Find the two exact values of k for which l2 is a tangent to C.
Core 12 Mathematics Edexcel January 2015 Question 14
In this question, solutions based entirely on graphical or numerical methods are not acceptable.
(i) Solve, for 0 ≤ x < 360°,
3sin x + 7cos x = 0
Give each solution, in degrees, to one decimal place.
(ii) Solve, for 0 ≤ θ < 2π,
10 cos2θ + cos θ = 11sin2θ – 9
Give each solution, in radians, to 3 significant figures.
Core 12 Mathematics Edexcel January 2015 Question 15
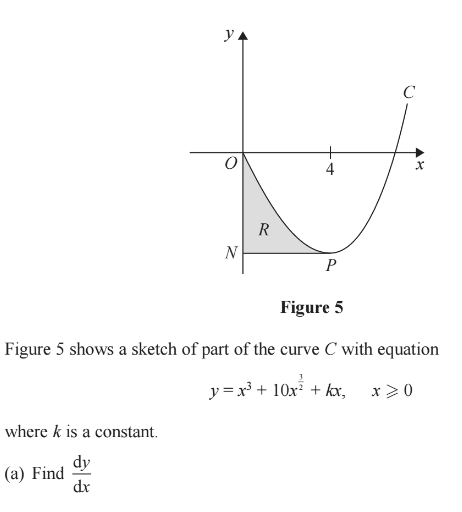
The point P on the curve C is a minimum turning point.
Given that the x coordinate of P is 4
(b) show that k = –78
The line through P parallel to the x-axis cuts the y-axis at the point N.
The finite region R, shown shaded in Figure 5, is bounded by C, the y-axis and PN.
(c) Use integration to find the area of R.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.