Equality Of Matrices

Two matrices are considered equal if and only if they meet both of the following conditions:

1. Same Dimensions (Order): They must have the same number of rows and the same number of columns.
2. Corresponding Elements are Equal: Every element in the same position in both matrices must have the same value.

The following diagram shows examples of matrices .

Let’s illustrate with examples:

Two matrices are equal if they have the same dimension or order and the corresponding elements are identical.

 

 

Matrices P and Q are equal.

 

 

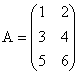
Matrices A and B are not equal because their dimensions or order is different.

We can use the equality of matrices to solve for variables.

Example:
Given that the following matrices are equal, find the values of x, y and z .

 

Solution:
Equate the corresponding elements and solve for the variables.

x + 3 = 6
x = 3

y = −1

z − 3 = 4
z = 7

Equal Matrices and solving variables
Two matrices are equal if they have the same dimensions and all corresponding elements are equal.

• Show Video Lesson

How to solve variables in equal matrices (equivalent matrices)?

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.