Every Line is a Graph of a Linear Equation

Examples, solutions, videos to help Grade 8 students learn that any non-vertical line is the graph of a linear equation in the form of y = mx + b, where b is a constant.

New York State Common Core Math Grade 8, Module 4, Lesson 20

Worksheets for Grade 8

Lesson 20 Student Outcomes

• Students know that any non-vertical line is the graph of a linear equation in the form of y = mx + b, where b is a constant.
• Students write the equation that represents the graph of a line.

Lesson 20 Summary

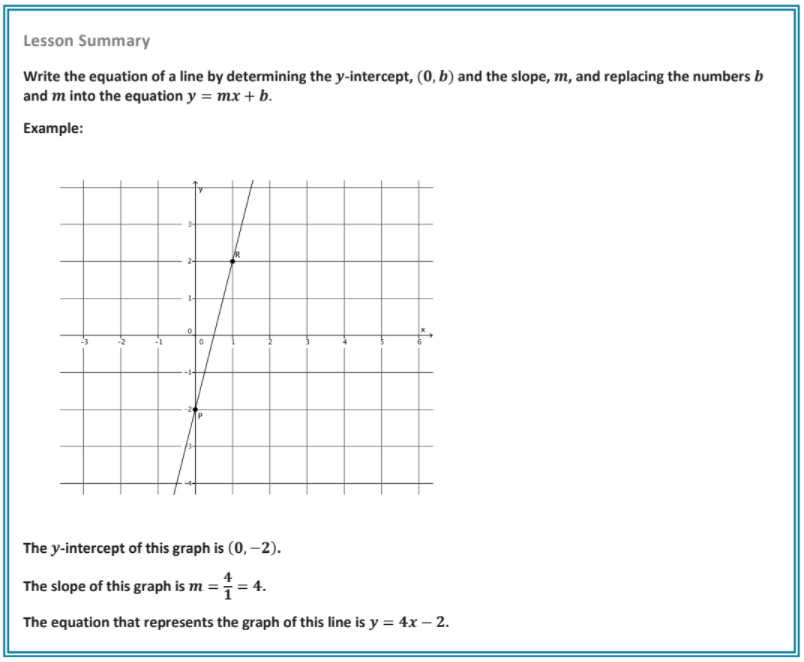
• Write the equation of a line by determining the y-intercept, (0, b) and the slope, m, and replacing the numbers b and m into the equation y = mx + b.

 

Lesson 20 Opening Exercise
Find the equations of the lines for graph 1 and graph 2.
Examples
Given the graph of a line, we want to be able to write the equation that represents it.
Which form of a linear equation do you think will be most valuable for this task, the standard form ax + by = c, or slope-intercept form y = mx + b.
Write the equation that represents the graph of the line shown below:
First, identify the y-intercept.
Now we must use what we know about slope to determine the slope of the line.
What fraction represents the slope of this line?
What must the equation of the line be?

Exercises 1 - 4
Write the equation that represents the line shown.
Use the properties of equality to change the equation from slope intercept form, y= mx + b, to standard form, ax + by = c, where a, b, and c are integers and a is not negative.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.