Even and Odd Functions
Related Pages
More Lessons for Grade 2 Math
Math Worksheets
Examples, solutions, videos, activities and worksheets that are suitable for A Level Maths. In this lesson, we will look into even and odd functions.
What is an Even Function?
Definition:
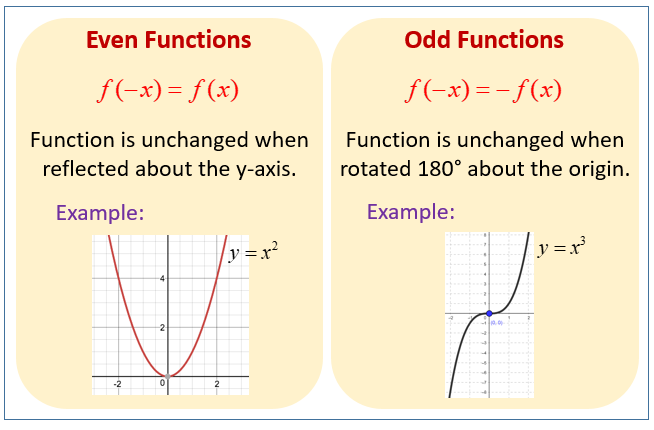
A function f(x) is even if f(-x) = f(x) for all x in its domain.
Graphical Interpretation:
The graph of an even function is symmetric with respect to the y-axis. This means that if you reflect the graph across the y-axis, it remains unchanged. This means that plugging in a negative x-value gives you the same y-value as plugging in the positive x-value.
Examples:
f(x) = x²
f(x) = cos(x)
f(x) = |x| (absolute value of x)
What is an Odd Function?
Definition:
A function f(x) is odd if f(-x) = -f(x) for all x in its domain.
Graphical Interpretation:
The graph of an odd function is symmetric with respect to the origin. This means that if you rotate the graph 180 degrees about the origin, it remains unchanged.
Examples:
f(x) = x³
f(x) = sin(x)
f(x) = x
Neither:
If a function does not satisfy either of the above conditions, it is neither even nor odd.
How to determine if a function is even, odd, or neither?
The following diagrams show how to distinguish between even and odd functions. Scroll down the page for more examples and solutions.
Graphical Test
- The graph of an even function is symmetric with respect to the y-axis.
- The graph of an odd function is symmetric with respect to the origin.
Algebraic Test
- If f(-x) is exactly the same as the original function f(x), then the function is even.
- If f(-x) is exactly the negative of the original function f(x), then the function is odd.
- If neither of these conditions is met, then the function is neither even nor odd.
Determining if a Function is Even, Odd or Neither
Even and Odd Functions
How to determine if a function is even, odd, or neither?
Examples of Even and Odd Functions
How to algebraically determine whether a function is even, odd or neither.
Determine if a function is even, odd, or neither. Mostly algebraic with two basic graphic examples.
Recognizing Odd and Even Functions
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.