Exponent Rules
Related Pages
Exponents
Rules Of Exponents
Logarithmic Functions
More Math Lessons
In these lessons, we will learn five rules of exponent and how to use them. These exponent rules are typically covered in Grade 7 Math.
Exponent rules (also called laws of exponents) are a set of rules that simplify expressions involving exponents.
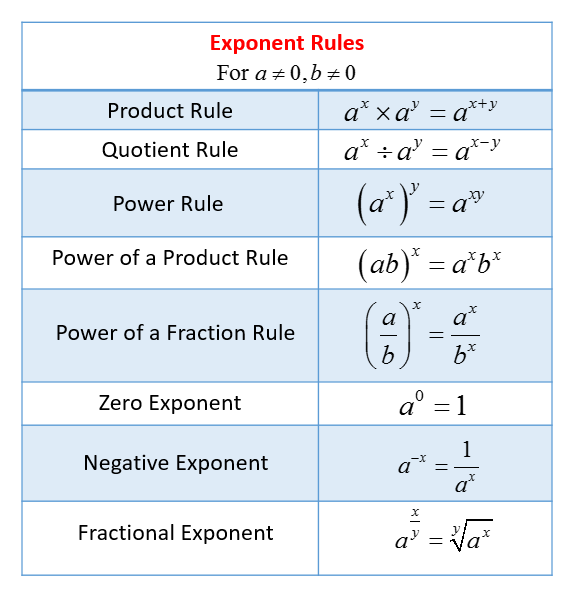
The following table give the Exponent Rules. Scroll down the page for examples and solutions.
The rules of exponent are:
Product Rule:
xm × xn = xm+n
When we multiply two powers that have the same base, we add the exponents.
Example: 32 x 35 = 37
Power Rule:
(xm)n = xm × n
When we raise a power to a power, we multiply the exponents.
Example: (32)5 = 310
Quotient Rule:
xm / xn = xm-n (where x ≠ 0)
When we divide two powers with the same base, we subtract the exponents.
Example: 36 ÷ 32 = 34
Zero Rule:
x0 = 1 (where x ≠ 0)
Any nonzero number raised to the power of zero equals 1.
Example: 540 = 1
Negative Rule:
x-n = 1 / xn (where x ≠ 0)
Any nonzero number raised to a negative power equals its reciprocal raised to the opposite positive power.
Example: 2-3 = 1/(23)
Fractional Exponent Rule (Roots):
xm/n = n√xm = (n√x)m
A fractional exponent represents a root. The denominator of the fraction is the index of the root, and the numerator is the power.
Example: x1/2 = √x (square root)
x2/3 = 3√x2 = (3√x)2
Key Points to Remember:
- The base must be the same to use the product and quotient rules.
- A negative exponent does not make the number negative. It creates a reciprocal.
- Fractional exponents represent roots.
Introduction To Exponent Rules
Exponent Rules Song
Learn exponent rules through music!
Basic Exponent Properties
This video will illustrate the rules with a few examples.
Simple Rules Of When To Add Or Multiply The Exponents In Common Bases
Rules Of Exponents Set To Music
How To Apply The Rules Of Exponents?
Example:
Simplify the following expressions:
a) (2x34)(3xy5)2
b) (x5y9)(-5x2y2)4
Example:
Simplify the following expressions:
a) (x2/2)4
b) (4n6)2
Example:
Simplify the following expressions:
a) (3x2y4)5/(3x3y7)3
b) (5xy2)4/(5x2y)6
How To Evaluate Expressions With Negative Exponents?
Example:
Simplify the following expressions:
a) (8a6b-4)/(24a-8b9)
b) (10a2b6)(50a-3b-4)
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.