Introduction to Logarithmic Functions

In this lesson, we will look at what are logarithms and the relationship between exponents and logarithms.
Logarithms can be considered as the inverse of exponents (or indices).

Definition of Logarithm

If a^x = y such that a > 0, a ≠ 1 then log_a y = x

a^x = y ↔ log_a y = x

Exponential Form

y = a^x

Logarithmic Form

log_a y = x

Remember: The logarithm is the exponent.

The following diagram shows the relationship between logarithm and exponent. Scroll down the page for more examples and solutions for logarithms and exponents.

Example:

Convert the following exponential form to the logarithmic form:
a) 4² = 16
b) 2⁵ = 32
c)

Solution:

a) 4² = 16
2 = log₄ 16 (the log is the exponent)
b) 2⁵ = 32
5 = log₂ 32

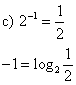
Example:

Convert the following logarithmic form to exponential form
a) 3 = log₂ 8
b) 2 = log₅ 25
c)

Solution:

a) 3 = log₂ 8
2³ = 8
b) 2 = log₅ 25
5² = 25

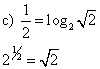
Take note of the following:

• Since a¹ = a, log_a a = 1
• Since a⁰ = 1, log_a 1 = 0
• Log*_a* 0 is undefined
• Logarithms of negative numbers are undefined.
• The base of logarithms can be any positive number except 1.
• Logarithms to the base 10 are known as common logarithms and are represented by log₁₀ or log.
• Logarithms to the base e are known as natural logarithms and are represented by log_e or ln.

Function Notation with Logs and Exponentials
Function notation is used frequently in science to express functions that contain logs and exponents. We learn to use function notation with logs and exponentials in order to solve problems such as computing compounding interest. We can solve these problems written in function notation with logs and exponentials using techniques from solving exponential and log equations.

• Show Step-by-step Solutions

Logarithm - Solving log & exponent equations
This video provides an introduction to solving logarithmic and exponential equations. A methodology is introduced so that students will have some type of basic strategy for solving these types of equations.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.