Exponents and Roots - GRE

Related Pages
Exponents
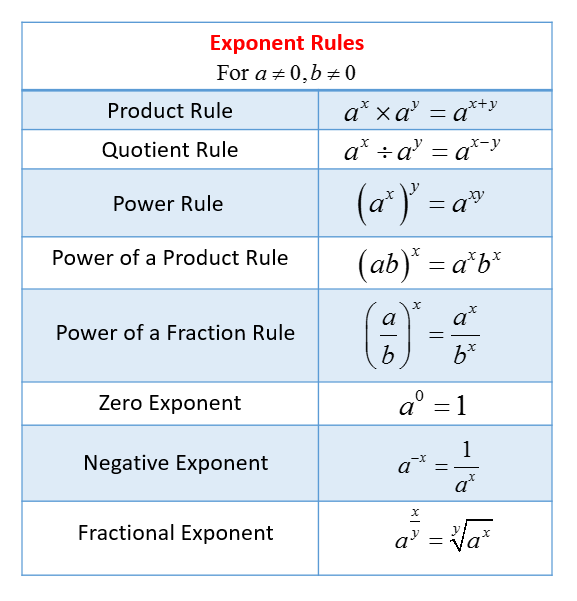
Exponent Rules
Logarithmic Functions
More Math Lessons

Exponents

Exponents are used to denote the repeated multiplication of a number by itself.

The following are some rules of exponents. Scroll down the page for more examples and solutions.

• Worksheets to Practice Exponent Rules

  Printable
  Product Rule
  Quotient Rule
  Power Rule
  Negative Exponents
  Fractional exponents
  Laws of Exponents
  

  Online
  Apply Law of Exponents (multiply)
  Apply Law of Exponents (mixed)
  

Free Exponent Games Online
Multiply Exponents	Divide Exponents	Power of a Power
Power of a Product	Negative Exponents	Fractional Exponents

 

For example, 2⁴ = 2 × 2 × 2 × 2 = 16
In the expression, 2⁴, 2 is called the base, 4 is called the exponent, and we read the expression as “2 to the fourth power.”

When the exponent is 2, we call the process squaring.

For example,
5² = 25, is read as "5 squared is 25".
6² = 36, is read as "6 squared is 36".

When negative numbers are raised to powers, the result may be positive or negative. A negative number raised to an even power is always positive, and a negative number raised to an odd power is always negative.

For example,
(−3)⁴ = −3 × −3 × −3 × −3 = 81
(−3)³= −3 × −3 × −3 = −27

Take note of the parenthesis: (−3)² = 9, but −3² = −9

Zero or Negative Exponents

Exponents can also be negative or zero; such exponents are defined as follows.

• For all nonzero numbers a, a⁰ = 1.
• The expression 0⁰ is undefined.
• For all nonzero numbers a,

Take note that

How to work with zero and negative exponents?

• Show Video Lesson

Square Roots

A square root of a nonnegative number n is a number r such that r² = n.

For example, 5 is a square root of 25 because 5² = 25.

Another square root of 25 is −5 because (−5)² is also equals to 25.

The symbol used for square root is . (The symbol is also called the radical sign).

Every positive number a has two square roots: √a, which is positive, and -√a, which is negative.
√16 = 4 and −√16 = −4

The only square root of 0 is 0. Square roots of negative numbers are not defined in the real number system.

Perfect squares and square roots

Some numbers are called perfect squares. It is important we can recognize perfect square when working with square roots.
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100

• Show Video Lesson

Rules for Square Roots

Here are some important rules regarding operations with square roots, where x > 0 and y > 0

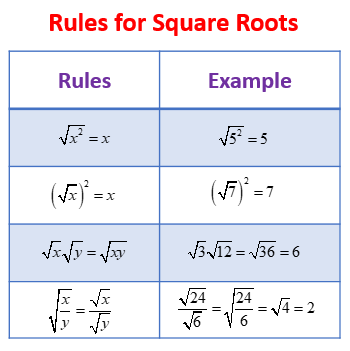
Product Rule & Simplifying Square Roots

Examples:
Simplify
√18
√48
³√2 ˙ ³√4
³√54

• Show Video Lesson

Quotient Rule & Simplifying Square Roots

• Show Video Lesson

How to use the rules regarding operations with square roots?

• Show Video Lesson

Roots of Higher Order

A square root is a root of order 2. Higher-order roots of a positive number n are defined similarly.

The cube root is a root of order 3.

For Example:
8 has one cube root. The cube root of 8 is 2 because 2³ = 8.
−8 has one cube root. The cube root of −8 is −2 because (−2)³ = −8

The fourth root is a root of order 4.

For example,
8 has two fourth roots. because 2⁴ = 16 and (−2)⁴ = 16

These n^th roots obey rules similar to the square root.

There are some notable differences between odd order roots and even-order roots (in the real number system):

• For odd-order roots, there is exactly one root for every number n, even when n is negative. For example, the cube root of 8 is 2 and the cube root of −8 is −2.
• For even-order roots, there are exactly two roots for every positive number n and no roots for any negative number n. For example, the fourth root of 16 is 2 and −2 and there is no fourth root for −16.

What are radicals and how to simplify perfect square, cube, and nth roots?

• Show Video Lesson

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.