Angle Properties - Find the Angle Problems
These lessons give a summary of the different angle properties and how they can be used to find missing angles.
Related Pages
Pairs Of Angles
Corresponding Angles
Alternate Interior Angles & Alternate External Angles
More Geometry Lessons
“Find the angle” problems are very common in tests like the SAT, GRE or the GCSE. In such problems, you will be given some lines and angles and you will be required to find a particular angle or angles.
In order to answer this type of questions,
- you would need to know some commonly used angle properties.
- you would need to practice lots of such problems. The more you practice, the easier it becomes to “see” which properties need to be applied.
Some Common Angle Properties
The sum of angles at a point is 360˚.
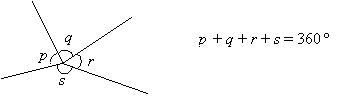
Vertical angles are equal.
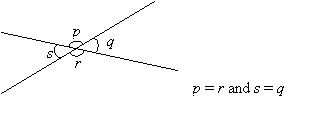
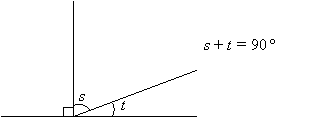
The sum of complementary angles is 90˚.
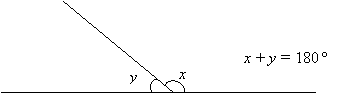
The sum of angles on a straight line is 180˚.
Alternate Angles
(Angles found in a Z-shaped figure)
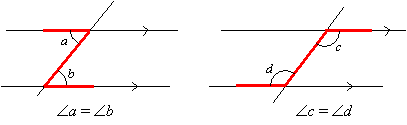
Corresponding Angles
(Angles found in a F-shaped figure)
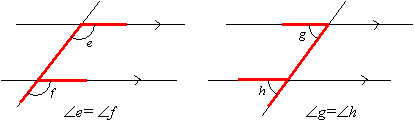
Interior Angles
(Angles found in a C-shaped or U-shaped figure)
Interior angles are supplementary. Supplementary angles are angles that add up to 180˚.
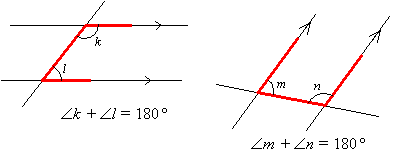
The sum of angles in a triangle is 180˚.
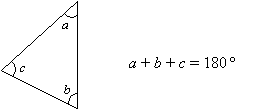
An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
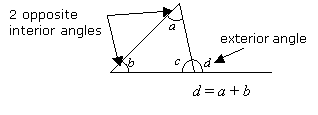
The sum of interior angles of a quadrilateral is 360˚.
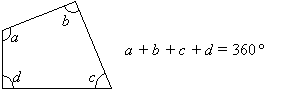
How to use the above angle properties to solve some “find the angle” problems?
Find the Measure of the Missing Angle
Angles and Parallel Lines : solving problems
Finding missing angles on two parallel lines, using corresponding angles and angles in a triangle.
Angles formed by Parallel Lines and Transversals
How to use Properties of Vertical Angles, Corresponding Angles, Interior Angles of a Triangle, and Supplementary Angles to find all the angles in a diagram. Other Properties discussed include Alternate Interior Angles, Alternate Exterior Angles, Complementary Angles, and the Exterior and Opposite Interior Angles of a triangle.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.