SAT Practice Test 3, Section 2: Questions 1 - 5

Related Topics:
More Lessons for SAT Test Preparation

Math Worksheets

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

1. Correct answer: (D)

Given:
3x + 9 = 5x + 1

To find:
The value of x

Solution:
Topic(s): Isolate variable

3x + 9 = 5x + 1 ⇒ 2x = 8 ⇒ x = 4

Answer: (D) 4

2. Correct answer: (B)

Given:
7, 15, 31, 63, …
First term is 7
Each term after the first is determined by multiplying the preceding tem by m and then adding p

To find:
The value of m

Solution:
Topic(s): Number sequence problems

From the given sequence, we can obtain these 2 equations.

(2 equations will be enough since we have to solve 2 variables)

7m + p = 15 (equation 1)
15m + p = 31 (equation 2)

Subtract equation 1 from equation 2

8m = 16 ⇒ m = 2

Answer: (B) 2

3. Correct answer: (B)

Given:
T-shirts with 3 different colors and 4 different sizes

To find:
The number of different combinations of color and size possible

Solution:
Topic(s): Permutations

To get the different combinations, we need to multiply the different colors possible with the different sizes possible.

3 × 4 = 12

Answer: (B) 12

4. Correct answer: (D)

To find:
Which of the given functions will result in f(-3) > f(3)

Solution:
Try to eliminate some answers by reasoning and then substitute to determine the others.

We can eliminate (B) because the result of the function is always 4

(– n)^y = n^y if y is an even number.

So, for (A) and (E), f(-3) = f(3). We can eliminate (A) and (E)

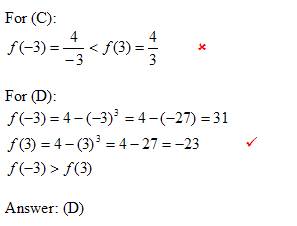
5, Correct answer: (E)

Given:
Force required to stretch a spring beyond its natural length is proportional to how far the spring is being stretched
Force of 15 pound stretches a spring 8 cm beyond its natural length

To find:
Force needed to stretch the spring 20 cm beyond its natural length

Solution:
Topic(s): Directly proportional problem

Rewrite the problem as

If 8 cm then 15 pound. If 20 cm then how many pounds?

8 → 15

20 →

Answer: (E) 37.5