Gauss-Jordan Method of Solving Matrices
Related Topics:
More Lessons on Matrices
Math Worksheets
Videos, worksheets, games and activities to help Algebra students learn how to use the Gauss-Jordan Method to Solve a System of Linear Equations.
The Gauss-Jordan method, also known as Gauss-Jordan elimination, is an algorithm for solving systems of linear equations. It is an extension of the Gaussian elimination method, where the matrix is further reduced until it is in reduced row echelon form (RREF). This form makes it straightforward to read off the solution to the system.
The following diagrams show how to solve a systems of equations using the Gauss-Jordan method. Scroll down the page for more
examples and solutions.
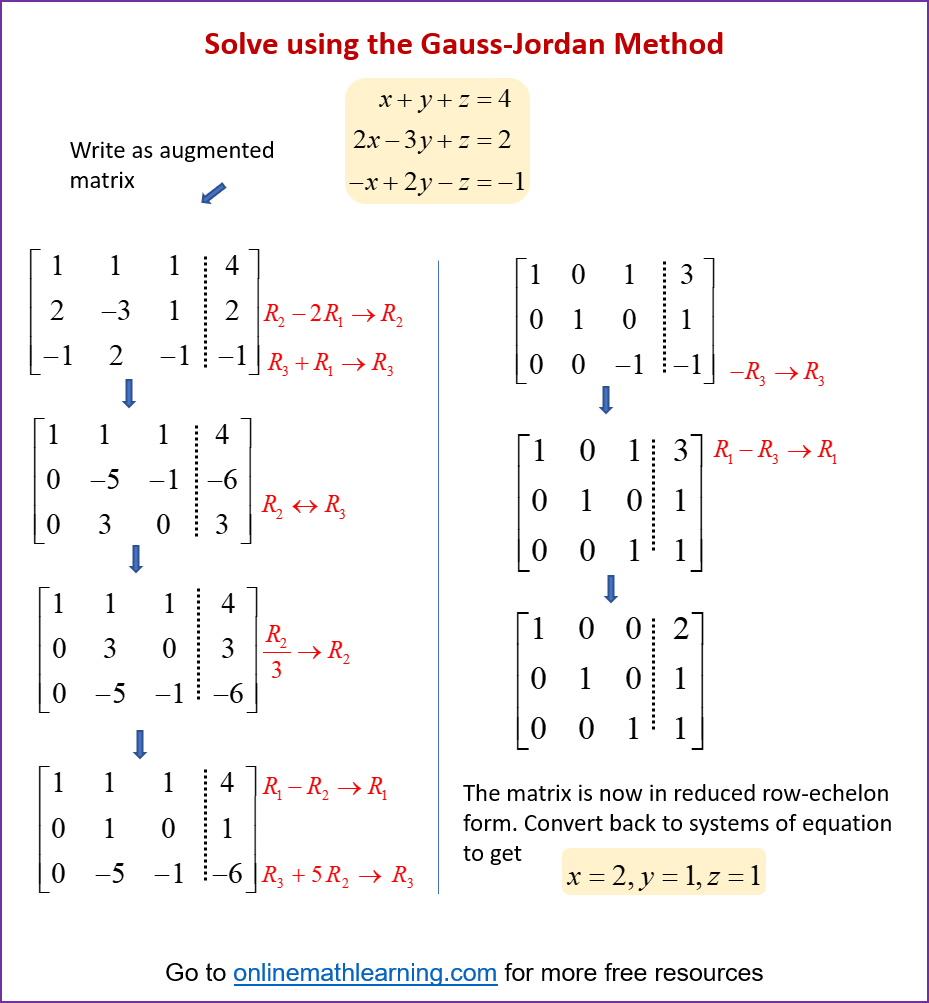
Steps of the Gauss-Jordan Method:
- Form the Augmented Matrix:
Represent the system of linear equations as an augmented matrix. This matrix includes the coefficients of the variables and the constants. - Apply Elementary Row Operations to Obtain Reduced Row Echelon Form (RREF):
The goal is to transform the augmented matrix into RREF using elementary row operations. A matrix is in RREF if it satisfies the following conditions:
a) All zero rows are at the bottom.
b) The first non-zero entry (leading entry or pivot) in each non-zero row is 1.
c) The leading 1 in any row is to the right of the leading 1’s in the rows above it.
d) Each column containing a leading 1 has zeros in all its other entries (both above and below the leading 1).
The allowed elementary row operations are:
a) Swap the position of two rows. (Notation: Ri ↔ Rj)
b) Multiply a row by a non-zero constant. (Notation: kRi → Ri)
c) Add a multiple of one row to another row. (Notation: Ri + kRj → Ri)
- Read the Solution from the Reduced Row Echelon Form: a) Once the augmented matrix is in RREF, the solution to the system of equations can be directly read from the matrix. b) If a row in the RREF looks like [0 0 … 0 | b] where b is non-zero, the system is inconsistent and has no solution. c) If there are rows with leading 1s, the corresponding variables are the basic variables, and their values are given by the numbers in the last column of those rows. d) If there are columns without leading 1s, the corresponding variables are free variables, and the system has infinitely many solutions.
Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 1
Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 2
This video explains how to solve a system of equations by writing an augmented matrix in reduced row echelon form. This example has one solution.
This video provides an example of how to solve a system of three linear equations with two unknowns by writing an augmented matrix in row echelon form. This example has one solution.
This video provides an example of how to solve a system of three linear equations with two unknowns by writing an augmented matrix in row echelon form. This example has no solution.
This video provides an example of how to solve a system of three linear equations with two unknowns by writing an augmented matrix in row echelon form. This example has infinite solutions.
Algebra - Matrices - Gauss Jordan Method Part 1 Augmented Matrix
Algebra - Matrices - Gauss Jordan Method Part 2 Augmented Matrix
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.