Congruent Triangles
Related Topics:
More Lessons for High School Geometry
More lessons for geometry
A series of free, online High School Geometry Video Lessons.
Videos, worksheets, and activities to help Geometry students.
Rules to determine Triangle Congruency
The following diagrams show the congruent triangles shortcuts: SSS, SAS, ASA, AAS and RHS. Take note that SSA is not sufficient for Triangle Congruency. Scroll down the page for more examples, solutions, and proofs.
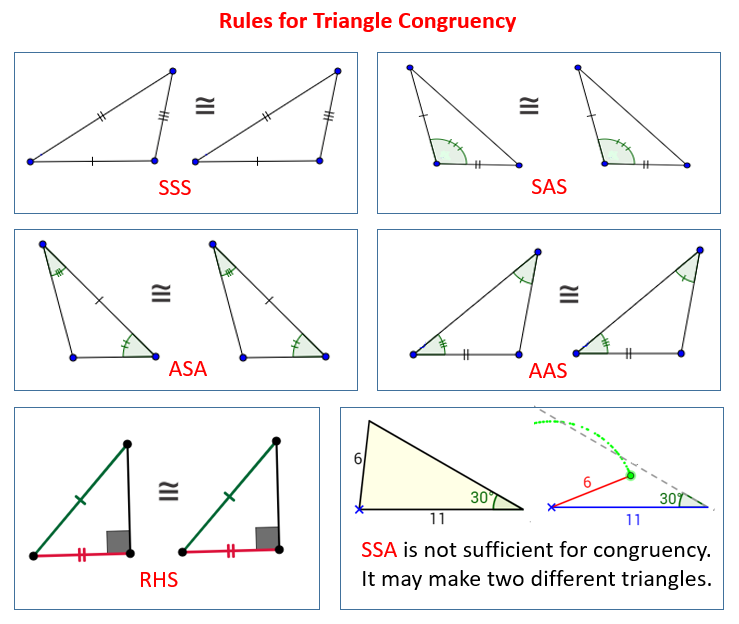
In these lessons, we will learn
- the congruent triangles shortcuts SSS and SAS Click here
- the congruent triangles shortcuts ASA and AAS Click here
- the congruent triangles shortcut Hypotenuse Leg Click here
- why SSA and AAA don’t work as congruence shortcuts Click here
SSS and SAS
When two triangles are congruent, all three pairs of corresponding sides are congruent and all three pairs of corresponding angles are congruent. If all three pairs of corresponding sides are congruent, the triangles are congruent. This congruence shortcut is known as side-side-side (SSS). Another shortcut is side-angle-side (SAS), where two pairs of sides and the angle between them are known to be congruent. SSS and SAS are important shortcuts to know when solving proofs
Triangle Congruence by SSS and SAS - How to Prove Triangles Congruent
Side Side Side Postulate
If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.
SAS Postulate
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
Triangle Congruence by SSS and SAS
How to use the SAS and SSS shortcuts to determine the congruence of two triangles?
ASA and AAS
If two triangles are congruent, all three corresponding sides are congruent and all three corresponding angles are congruent. If two pairs of corresponding angles and the side between them are known to be congruent, the triangles are congruent. This shortcut is known as angle-side-angle (ASA).
Another shortcut is angle-angle-side (AAS), where two pairs of angles and the non-included side are known to be congruent. ASA and AAS are important when solving proofs.
Proving triangles congruent using ASA postulate and AAS theorem
Proving triangles congruent using ASA postulate and AAS theorem
AAS, ASA, and HL Triangle Congruence
Hypotenuse Leg
In right triangles, if two legs are congruent and if the two hypotenuses are congruent, then the triangles are congruent. This is known as the hypotenuse leg theorem.
Note that this is the SSA shortcut which does not apply to non-right triangles. Applying the Pythagorean Theorem shows that only one value is possible for the other leg. Therefore, the two triangles are also congruent by the SAS or SSS congruence shortcut.
Hypotenuse - Leg Congruence Theorem
To prove triangles congruent by the hypotenuse leg theorem
Why SSA and AAA Don’t Work as Congruence Shortcuts
Four shortcuts allow students to know two triangles must be congruent: SSS, SAS, ASA, and AAS. Knowing only side-side-angle (SSA) does not work because the unknown side could be located in two different places. Knowing only angle-angle-angle (AAA) does not work because it can produce similar but not congruent triangles.
How to determine which congruence shortcuts do not work and why
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.