Centers of Triangles
Related Topics:
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Lessons.
Examples, solutions, videos, worksheets, and activities to help Geometry students.
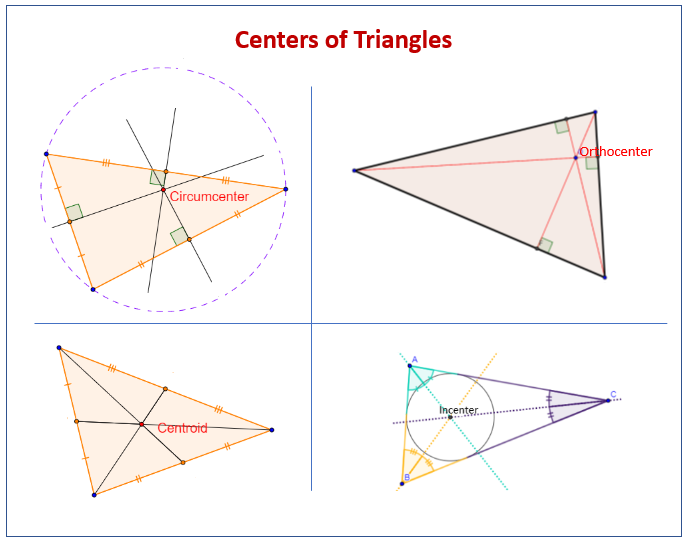
In this lesson, we will look at the four common centers of triangles: circumcenter, orthocenter, centroid and incenter.
The following diagram shows four centers of triangles: circumcenter, orthocenter, centroid and incenter. Scroll down the page for more examples and solutions.
We will learn
- how to construct the circumcenter of a triangle Click here
- how to construct the orthocenter of an acute triangle and an obtuse triangle Click here
- how to construct the centroid or center of gravity of a triangle Click here
- how to construct the incenter of a triangle Click here
Constructing the Circumcenter
The point of concurrency of the three perpendicular bisectors of a triangle is the circumcenter. It is the center of the circle circumscribed about the triangle, making the circumcenter equidistant from the three vertices of the triangle. The circumcenter is not always within the triangle. In a coordinate plane, to find the circumcenter we first find the equation of two perpendicular bisectors of the sides and solve the system of equations.
How to construct the circumcenter using a compass and straightedge?
Using compass and straightedge to construct the circumcenter of a triangle.
Constructing the Orthocenter
The orthocenter is the point of concurrency of the altitudes in a triangle. A point of concurrency is the intersection of 3 or more lines, rays, segments or planes. The orthocenter is just one point of concurrency in a triangle. The others are the incenter, the circumcenter and the centroid.
How to construct the orthocenter of a triangle?
Using a straight edge and compass to create the orthocenter of an acute triangle
Using a straight edge and compass to create the external orthocenter of an obtuse triangle
Constructing the Centroid
The centroid is the point of concurrency of the three medians in a triangle. It is the center of mass (center of gravity) and therefore is always located within the triangle. The centroid divides each median into a piece one-third the length of the median and two-thirds the length. To find the centroid, we find the midpoint of two sides in the coordinate plane and use the corresponding vertices to get equations.
How to identify the centroid and the way it divides each of the medians?
Using a straight edge and a compass to create the centroid or center of gravity of a triangle
Constructing the Incenter
The incenter is the point of concurrency of the three angle bisectors of a triangle. It is the center of the circle that can be inscribed in the triangle, making the incenter equidistant from the three sides of the triangle. The incenter is always located within the triangle.
How to construct the incenter of a triangle by constructing angle bisectors?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.