Geometry Constructions
Related Topics:
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Video Lessons and solutions.
Examples, solutions, videos, worksheets, and activities to help Geometry students.
How to duplicate a line segment using a compass and straightedge? How to use a compass and straightedge to construct a congruent segment?
How to duplicate an angle using a compass and straightedge? How to use a compass and straightedge to construct a congruent angle?
How to define a perpendicular bisector? How to use a straight edge and a compass to bisect a segment?
Perpendicular Line(1) Construction
How to use a compass and straightedge to construct a perpendicular line through a point on the line?
Perpendicular Line(2) Construction
How to use a compass and straightedge to construct a perpendicular line through a point not on the line?
You can use the free Mathway calculator and problem solver below to practice Algebra or other math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Video Lessons and solutions.
Examples, solutions, videos, worksheets, and activities to help Geometry students.
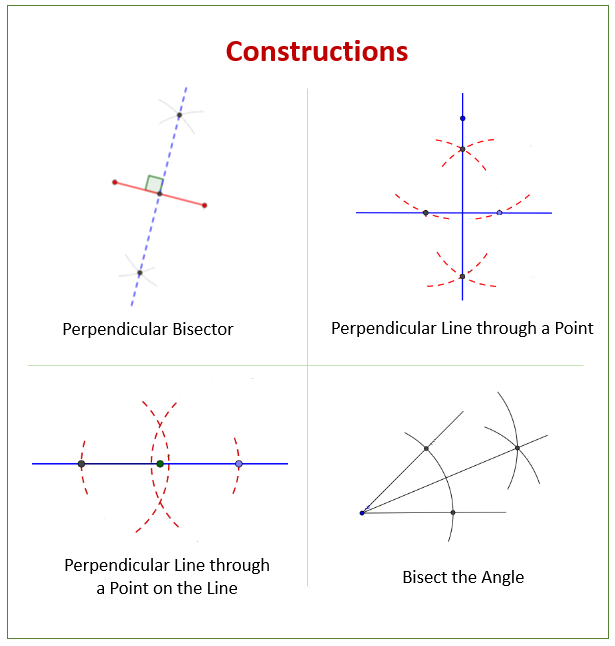
In these lessons, we will learn
- how to construct and duplicate a line segment
- how to construct and duplicate an angle
- how to construct a perpendicular bisector
- how to construct a perpendicular line through a point on the line
- how to construct a perpendicular line through a point not on the line.
Duplicating a Line Segment
When constructing a line segment, we use a compass and straightedge to first draw a ray or line and then a point that will serve as an endpoint of the new segment. Next, we measure the given segment with a compass and make a mark with the pencil end. Without changing the spacing of the compass, place the sharp end of the compass on the point drawn on the new line/ray, and make a mark on the line/ray.How to duplicate a line segment using a compass and straightedge? How to use a compass and straightedge to construct a congruent segment?
Duplicating an Angle
When constructing an angle, first swing an arc from the vertex of your angle. Then, swing a congruent arc from the new vertex. Return to the original angle; the drawn arc intersected the sides of the angle - measure this distance. On the new angle, place the sharp end of the compass on the intersection of the arc and ray and draw another arc. Draw a ray connecting the new vertex with the point of intersection.How to duplicate an angle using a compass and straightedge? How to use a compass and straightedge to construct a congruent angle?
Constructing the Perpendicular Bisector
When looking at a line segment, there is only one line that will pass through the midpoint that will be a constant distance between the two endpoints. This line is called the perpendicular bisector. To construct the perpendicular bisector, we first find the midpoint of the line segment and then use a compass and straightedge to draw the perpendicular line.How to define a perpendicular bisector? How to use a straight edge and a compass to bisect a segment?
Constructing a Perpendicular at a Point on a Line
When constructing a perpendicular bisector, we are specifically being asked to construct a line perpendicular to a line through the midpoint. To construct a perpendicular to a line through a point like the midpoint, we use a process similar to constructing a perpendicular to a line through a point not on the line. To construct a perpendicular, we use a compass and straightedge to determine a point equidistant from two equidistant points on the line.Perpendicular Line(1) Construction
How to use a compass and straightedge to construct a perpendicular line through a point on the line?
Constructing a Perpendicular to a Line
The shortest distance between a point not on a line and a line is along the perpendicular to the line. Constructing a perpendicular to a line uses the same process as constructing the perpendicular bisector of a line segment, but with one additional step. The first step is to swing an arc from the point and intersect the line in two places, which creates a segment that can be bisected.Perpendicular Line(2) Construction
How to use a compass and straightedge to construct a perpendicular line through a point not on the line?
Rotate to landscape screen format on a mobile phone or small tablet to use the Mathway widget, a free math problem solver that answers your questions with step-by-step explanations.
You can use the free Mathway calculator and problem solver below to practice Algebra or other math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
