Identity Matrix
Related Pages
Inverse Matrix
More Lessons on Matrices
More Lessons for Algebra
Math Worksheets
These lessons, with videos, examples and step-by-step solutions help Algebra students learn about the identity matrix.
The identity matrix is a special type of square matrix (a matrix with the same number of rows and columns). It plays a role in matrix multiplication similar to the number “1” in regular multiplication.
An identity matrix is a square matrix with the following properties:
- All the elements on the main diagonal (the diagonal from the top-left to the bottom-right) are equal to 1.
- All other elements (those off the main diagonal) are equal to 0.
Notation:
The identity matrix is usually denoted by the letter I or sometimes In, where n indicates the size of the matrix (number of rows and columns).
The following diagrams show examples of Identity Matrices and their properties. Scroll down the page for more examples and solutions of Identity Matrices.
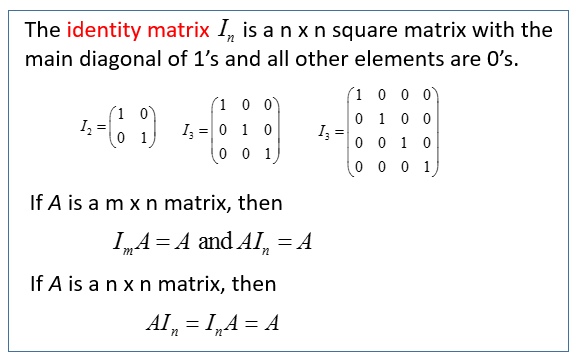
Key Property: Multiplication
The most important property of the identity matrix is its behavior in matrix multiplication:
When you multiply any matrix A by the identity matrix I (of compatible dimensions), the result is always the original matrix A.
AI = IA = A
The Identity Matrix
When dealing with matrix computation, it is important to understand the identity matrix.
We can think of the identity matrix as the multiplicative identity of square matrices,
or the one of square matrices. Any square matrix multiplied by the identity matrix of
equal dimensions on the left or the right doesn’t change. The identity matrix is used
often in proofs, and when computing the inverse of a matrix.
This video introduces the identity matrix and illustrates the properties of the identity matrix.
Learn what is an Identity Matrix
2×2 Identity Matrix
Identity Matrix
Identity Matrix
The Identity Matrix is a square matrix with zeros everywhere except on the main diagonal,
which has all elements equal to one. It is the product of a matrix and its inverse.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.