Integration by Parts

The following figures give the formula for Integration by Parts and how to choose u and dv. Scroll down the page for more examples and solutions.

 

Where:
u is the first function (to be differentiated).
dv is the second function (to be integrated).

Choosing u and dv (The LIATE Rule):
The key to successfully using integration by parts lies in choosing appropriate functions for u and dv. A helpful guideline is the LIATE rule, which suggests prioritizing functions for u in the following order:

1. Logarithmic functions (ln(x), log(x), etc.)
   
2. Inverse trigonometric functions (arctan(x), arcsin(x), etc.)
   
3. Algebraic functions (x, x², x³, etc.)
   
4. Trigonometric functions (sin(x), cos(x), tan(x), etc.)
   
5. Exponential functions (eˣ, 2ˣ, etc.)
   

The function that appears earlier in the LIATE list is usually a good choice for u. The remaining part of the integrand (including dx) is then chosen as dv.

How to derive the rule for Integration by Parts from the Product Rule for differentiation?
The Product Rule states that if f and g are differentiable functions, then

 

Integrating both sides of the equation, we get

 

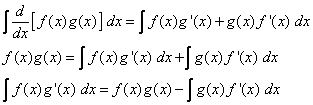
We can use the following notation to make the formula easier to remember.
Let u = f(x) then du = f‘(x) dx
Let v = g(x) then dv = g‘(x) dx

 

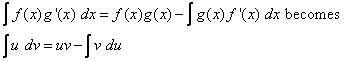
The formula for Integration by Parts is then

 

Example:
Evaluate
 

Solution:
Let u = x then du = dx

Let dv = sin xdx then v = –cos x

Using the Integration by Parts formula

 

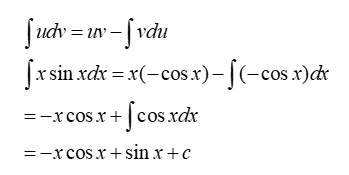
Example:
Evaluate
 

Solution:

 

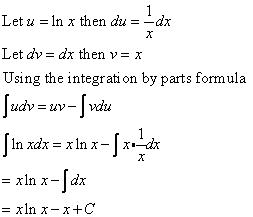
Example:
Evaluate
 

Let u = x² then du = 2x dx
Let dv = e^xdx then v = e^x

Using the Integration by Parts formula

 

We use integration by parts a second time to evaluate
 

Let u = x the du = dx

Let dv = e^x dx then v = e^x

 

Substituting into equation 1, we get

 

Integration by parts - choosing u and dv
How to use the LIATE mnemonic for choosing u and dv in integration by parts?
Let u be the first thing in this list and dv be everything else
Logarithmic functions
Inverse Trig functions
Algebraic functions
Trig functions
Exponential functions

Examples:
∫x⁵ln(x)dx
∫sin^-1(x)dx
∫e^xsin(x)dx
∫xe^xdx
∫x²cos(x)dx

• Show Video Lesson

Integration by Parts
3 complete examples are shown of finding an antiderivative using integration by parts.
Examples:
∫xe^-xdx
∫lnx - 1 dx
∫x - 5^xdx

• Show Video Lesson

Integration by Parts - Definite Integral

• Show Video Lesson

Evaluate a Indefinite Integral Using Integration by Parts
Example:
Use integration by parts to evaluate the integral:
∫ln(3r + 8)dr

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.