Long Division Of Polynomials

Long division of polynomials is a method used to divide one polynomial (the dividend) by another polynomial (the divisor). It is similar to numerical long division but we will use polynomials instead of just numerical values. It is particularly useful when the divisor is a polynomial of degree 1 or higher.

The following diagram shows an example of polynomial division using long division. Scroll down the page for more examples and solutions on polynomial division.

Steps for Polynomial Long Division

1. Arrange the polynomials:
   Write both the dividend and divisor in descending order of exponents.
   If any terms are missing (e.g., x³ + 1), insert placeholders with coefficients of zero (x³ + 0x² + 0x + 1).
   
2. Divide the first term of the dividend by the first term of the divisor to get the first term of the quotient.
3. Multiply the entire divisor by this term and write the result under the dividend.
4. Subtract this result from the dividend to get a new polynomial (the remainder).
5. Bring down the next term of the dividend and repeat the process until all terms are used.
6. Write the final answer, including any remainder as a fraction over the divisor.

• Printable & Online Polynomial Worksheets

  Add & Subtract Polynomials
  Multiply Polynomials
  Divide Polynomials
  

Example:
Evaluate (x² + 10x + 21) ÷ (x + 7) using long division.

Solution:
(x² + 10x + 21) is called the dividend and (x + 7) is called the divisor.

Step 1: Divide the first term of the dividend with the first term of the divisor and write the result as the first term of the quotient.

Step 2: Multiply that term with the divisor.

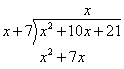
Step 3: Subtract and write the result to be used as the new dividend.

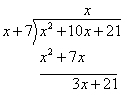
Step 4: Divide the first term of this new dividend by the first term of the divisor and write the result as the second term of the quotient.

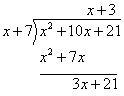
Step 5: Multiply that term and the divisor and write the result under the new dividends.

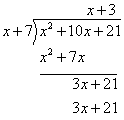
Step 6: Subtract to get the remainder.

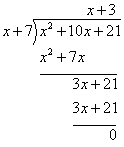
Note that it also possible that the remainder of a polynomial division may not be zero.

Example:
Evaluate (23y² + 9 + 20y³ – 13y) ÷ (2 + 5y² – 3y)

Solution:

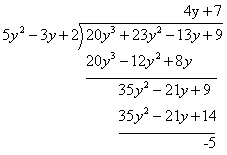
You may want to look at the lesson on synthetic division, a simplified form of long division.

Dividing Polynomials using Long Division
When dividing polynomials, we can use either long division or synthetic division to arrive at an answer. Using long division, dividing polynomials is easy. We simply write the fraction in long division form by putting the divisor outside of the bracket and the divided inside the bracket. After the polynomial division is set up, we follow the same process as long division with numbers.

Example:
(3x³ - 4x² + 2x - 1) ÷ (x + 1)

• Show Video Lesson

Dividing Polynomials by Binomials

Example:
(x² + 5x + 6) ÷ (x + 1)

• Show Video Lesson

Dividing Polynomials

Example:
(x² + 9x + 20) ÷ (x + 5)
(6x² + 7x - 20) ÷ (2x + 5)
(6x⁴ - 30x² + 24) ÷ (2x² - 8)
(3x⁵ + 4x³ - 5x + 8) ÷ (x² + 3)
(x⁵ + 2x⁴ + x³ - x² - 22x + 15) ÷ (x² + 2x - 3)

• Show Video Lesson

How to divide polynomials using long division?

Examples:

1. (5x³ - 6x² - 28x - 2) ÷ (x + 2)
2. (x³ - 1) ÷ (x - 1)

How to do Long Division with Polynomials with remainder?

Examples:

1. (x² + 7x + 12) ÷ (x + 3)
2. (15x² + 26x + 8) ÷ (5x + 2)
3. (4x² + 8x - 5) ÷ (2x + 1)

Key Points:
Placeholders: Don’t forget to use placeholders for missing terms.
Signs: Pay close attention to signs when subtracting.
Remainder: If you have a remainder, write it as a fraction over the divisor.
Check Your Work: You can check your answer by multiplying the quotient by the divisor and adding the remainder. This should give you the original dividend.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.