Matrix Addition and Subtraction
Related Topics: More Lessons on Matrices
In these lessons, we will learn how to add and subtract matrices.
We also have a Matrix Calculator that will allow you to add, subtract or multiply 2x2 matrices. Use it to check your answers.
Matrix addition and subtraction are fundamental operations in linear algebra. They are relatively straightforward, but there’s one key rule to remember: you can only add or subtract matrices that have the same dimensions. This means they must have the same number of rows and the same number of columns.
How to Add Matrices
To add two matrices, you simply add the corresponding elements (the elements in the same position) together.
How to Subtract Matrices
Matrix Subtraction works similarly to addition. You subtract the corresponding elements of the second matrix from the first matrix.
The following diagram gives some of examples adding and subtracting matrices. Scroll down the page for more examples and explanations.
Matrix Addition Examples
We can only add matrices of the same order.
Example:
Matrix addition is very simple; we just add the corresponding elements.
It is not possible to add matrices that do not have the same order, as shown in the following example:
How to add two matrices together?
If they both have the same dimensions (same number of rows and columns) then you just add up the numbers that are in the same spot.
Properties of Matrix Addition:
Commutative: A + B = B + A (The order in which you add matrices doesn’t matter.)
Associative: (A + B) + C = A + (B + C) (When adding three or more matrices, the grouping doesn’t matter.)
Matrix Subtraction Examples
Similarly, we can only subtract matrices of the same order.
Example:
We subtract the corresponding elements.
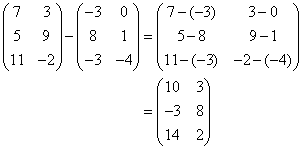
It is not possible to subtract matrices that do not have the same order as in the following example:
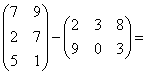
Introduction to matrices and examples of adding and subtracting matrices
Introduction to matrices
Define a matrix
A matrix is a rectangular arrangement or array of numbers called elements.
Identify the dimensions of a matrix
The dimension m × n of a matrix identifies how many rows and columns a specific matrix has. The number of rows is m and the number of columns is n.
Identify elements in a matrix
A number or element in a matrix is denoted aij, where i is the ith row and j is the jth column.
Perform matrix addition, subtraction and scalar multiplication
The sum of two matrices can only be found if both matrices have the same dimension. This means they must have the same number of rows and the same number of columns. To determine the sum, add corresponding elements.
The difference of two matrices can only be found if both matrices have the same dimension. To determine the difference, subtract corresponding elements.
How to add and subtract matrices?
Matrix Operations
Adding, Subtracting, and Multiplying by a constant for matrices is discussed.
Matrix Calculator
Enter in two 2x2 matrices and select addition, subtraction or multiplication.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.