Illustrative Mathematics Unit 6.1, Lesson 14: Nets and Surface Area
Learn about matching nets to their polyhedra and using nets to find the surface area of a polyhedron. After trying the questions, click on the buttons to view answers and explanations in text or video.
Return to the list of Illustrative Math lessons
Nets and Surface Area
Let’s use nets to find the surface area of polyhedra.
Illustrative Math Unit 6.1, Lesson 14 (printable worksheets)
14.1 - Matching Nets
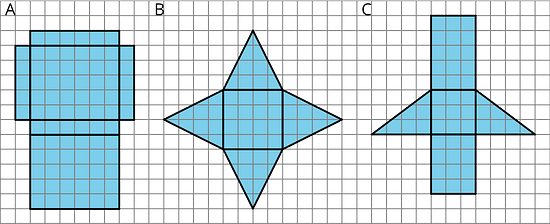
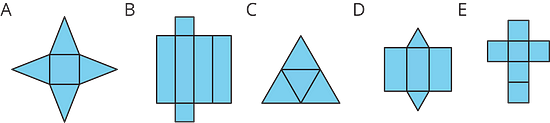
Each of the following nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.
14.2 - Using Nets to Find Surface Area
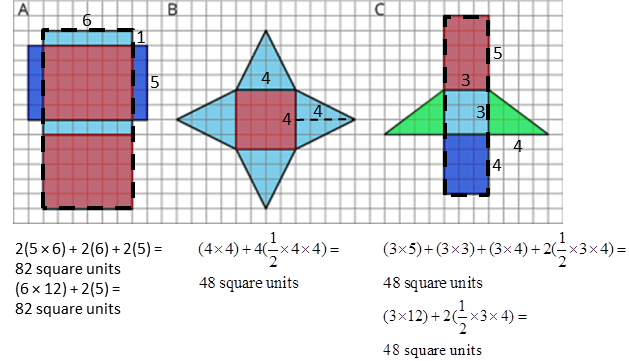
Your teacher will give you the nets of three polyhedra to cut out and assemble. Alternatively, you may print out the following nets.
-
Name the polyhedron that each net would form when assembled.
-
Cut out your nets and use them to create three-dimensional shapes.
-
Find the surface area of each polyhedron. Explain your reasoning clearly.
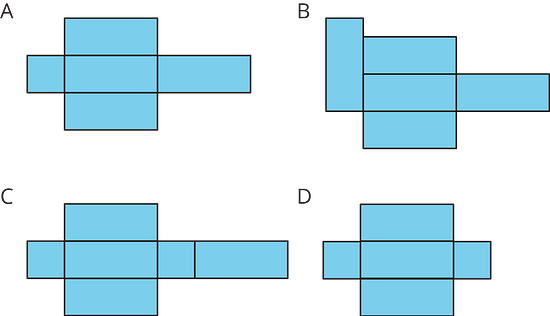
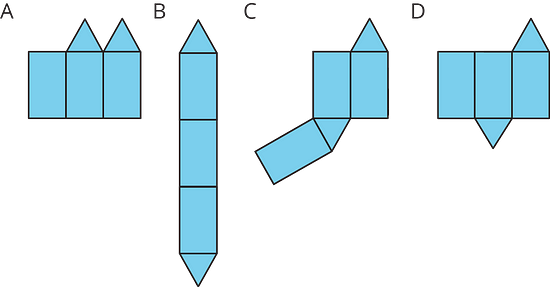
- For each net, decide if it can be assembled into a rectangular prism.
- For each net, decide if it can be assembled into a triangular prism.
Lesson 14 Summary
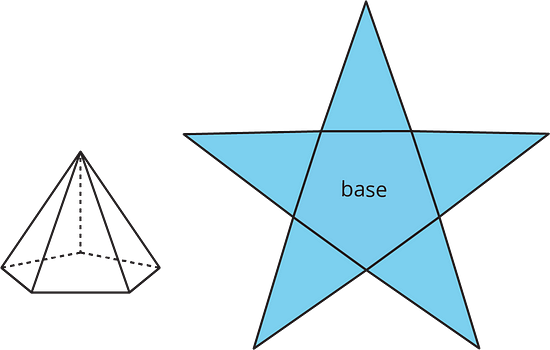
A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.
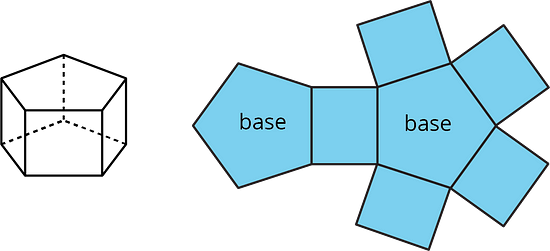
A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.
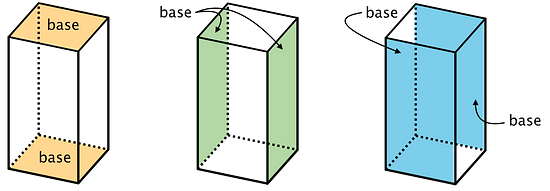
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.
Because a net shows all the faces of a polyhedron, we can use it to find its surface area.
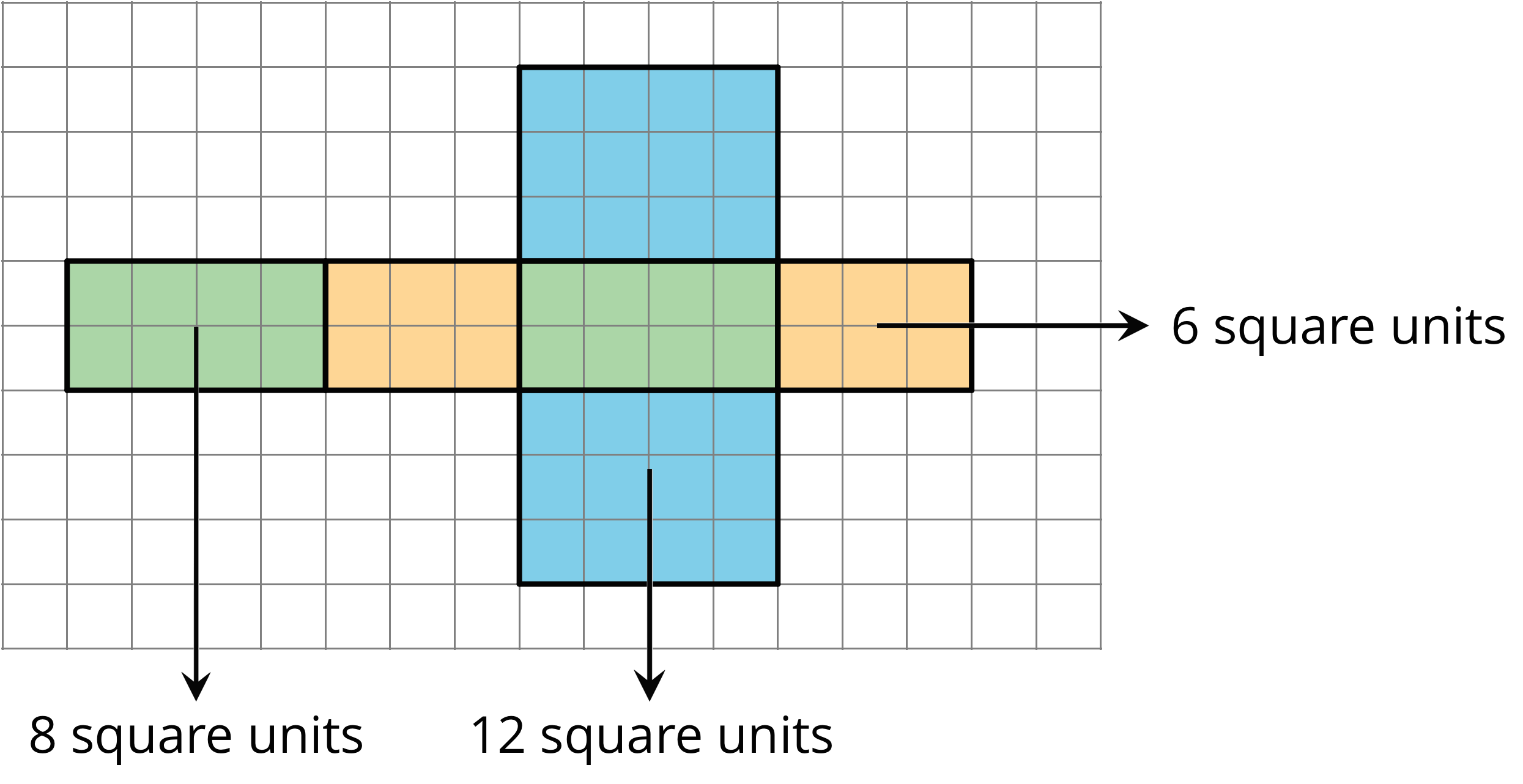
For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.
The surface area of the rectangular prism is 52 square units because 8 + 8 + 6 + 6 + 12 + 12 = 52.
Practice Problems
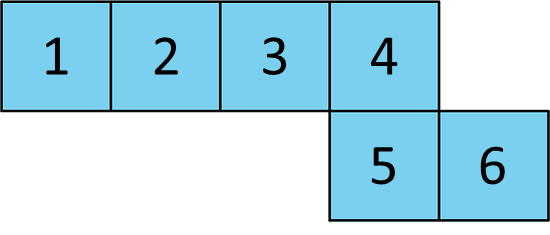
- Can the following net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.
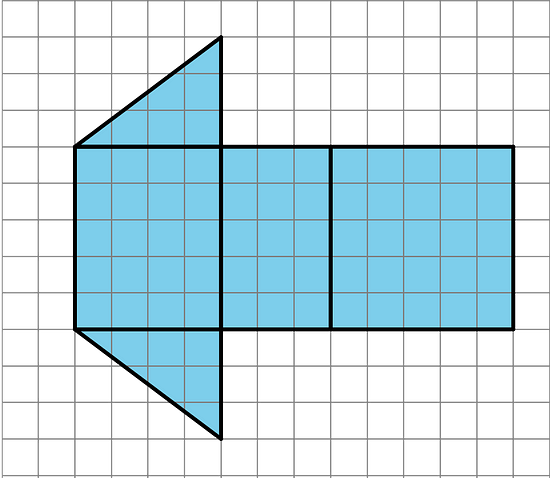
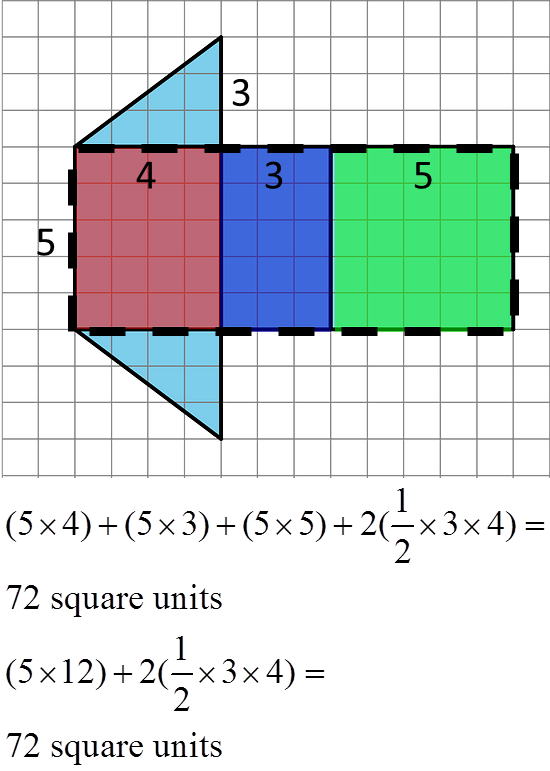
- a. What polyhedron can be assembled from this net? Explain how you know.
b. Find the surface area of this polyhedron. Show your reasoning.
- Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.
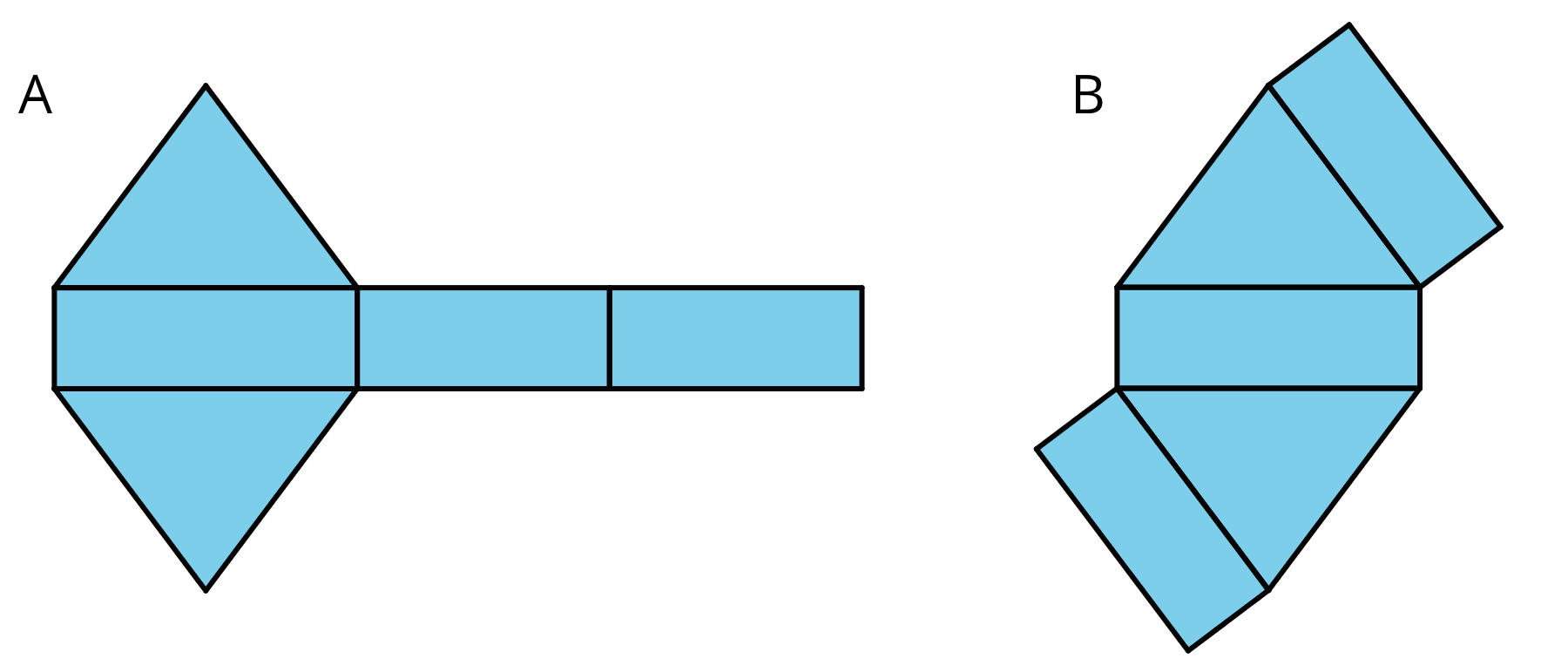
- Here are two three-dimensional figures.
Tell whether each of the following statements describes Figure A, Figure B, both, or neither.
a. This figure is a polyhedron.
b. This figure has triangular faces.
c. There are more vertices than edges in this figure.
d. This figure has rectangular faces.
e. This figure is a pyramid.
f. There is exactly one face that can be the base for this figure.
g. The base of this figure is a triangle.
h. This figure has two identical and parallel faces that can be the base.
- Select all units that can be used for surface area. Explain why the others cannot be used for surface area.
A. square meters
B. feet
C. centimeters
D. cubic inches
E. square inches
F. square feet
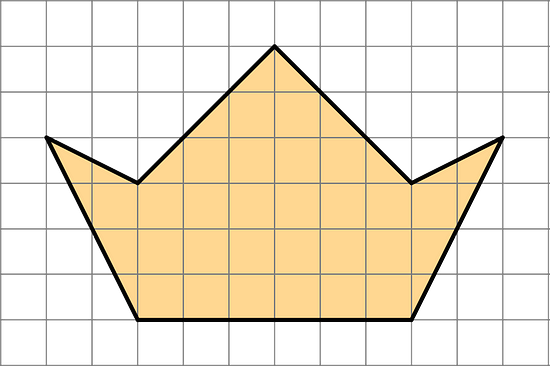
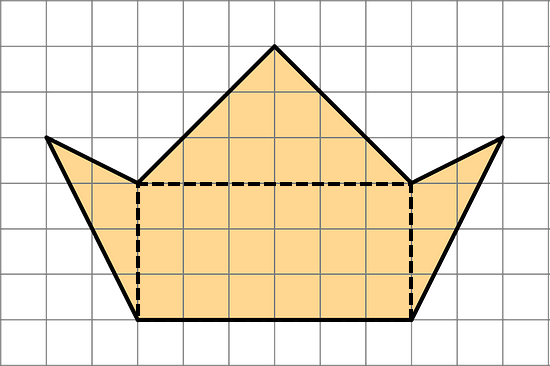
- Find the area of this polygon. Show your reasoning.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.