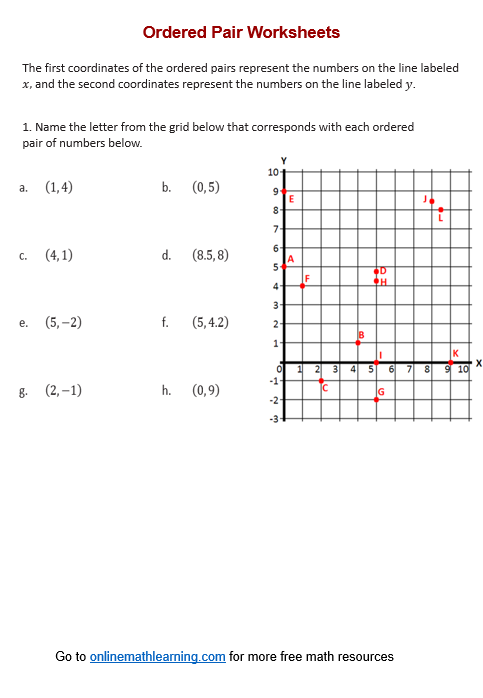
Ordered Pair Worksheet

Printable “Coordinate Geometry” Worksheets:
Plot Ordered Pairs (First Quadrant)
Ordered Pairs & Lines
Parallel Lines & Coordinate Plane

Ordered Pairs (Four Quadrants)
Symmetry in the Coordinate Plane
Coordinate Plane (Horizontal & Vertical Distance)

Free printable and online worksheets to help Grade 6 students learn how to use ordered pairs to name points in a grid and to locate points on a map or Cartesian plane. Identify the first number in an ordered pair as the first coordinate and the second number as the second coordinate. Understand the coordinate plane to include all four quadrants.

Ordered Pair

Ordered pairs are pairs of numbers written in a specific order, usually enclosed in parentheses and separated by a comma. In mathematics, ordered pairs are commonly used to represent points in the Cartesian coordinate system, where the first number in the pair represents the horizontal position (x-coordinate) and the second number represents the vertical position (y-coordinate).

Visualizing Ordered Pairs with Coordinate Planes or Cartesian Planes:
Imagine a grid with a horizontal number line (x-axis) at the bottom and a vertical number line (y-axis) on the left side. The point where these axes intersect is called the origin (0, 0). Positive values of x extend to the right, and negative values extend to the left. Positive values of y extend upwards, and negative values extend downwards.

Using Ordered Pairs to Locate Points:
Start at the Origin (0, 0): Imagine placing your finger at the point where the x and y axes intersect. This is the origin, represented by the ordered pair (0, 0).
Move Right (Positive x): If the first number (x-coordinate) in the ordered pair is positive, move that many units to the right from the origin along the x-axis.
Move Up (Positive y): If the second number (y-coordinate) in the ordered pair is positive, move that many units upwards from the starting point (after moving along the x-axis) along the y-axis.
Move Left (Negative x): If the first number (x-coordinate) is negative, move that many units to the left from the origin along the x-axis.
Move Down (Negative y): If the second number (y-coordinate) is negative, move that many units downwards from the starting point (after moving along the x-axis) along the y-axis.

Examples:
(3, 2): Move 3 units to the right (positive x) from the origin and then 2 units up (positive y). This point is located in the upper right quadrant of the graph.
(-2, 5): Move 2 units to the left (negative x) from the origin and then 5 units up (positive y). This point is located in the upper left quadrant of the graph.
(4, -1): Move 4 units to the right (positive x) from the origin and then 1 unit down (negative y). This point is located in the lower right quadrant of the graph.

Importance of Order:
The order of the numbers in an ordered pair is significant. For example, (2, 3) represents a different location than (3, 2) on the coordinate plane.

By understanding ordered pairs and their connection to coordinate planes, you can effectively represent points in two-dimensional space and solve problems involving geometric shapes and their properties.

Have a look at this video if you need to review ordered pairs.

• Ordered Pair

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Ordered Pair Worksheets.

 

More Ordered Pair Worksheets

Printable
(Answers on the second page.)
Ordered Pair Worksheet #1 (2 quadrants)
Ordered Pair Worksheet #2 (2 quadrants)
Ordered Pair Worksheet #3 (4 quadrants)
Ordered Pair Worksheet #4 (relate the points)

Related Lessons & Worksheets

Ordered Pair

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.