The Definition of a Parabola
Related Topics:
Lesson Plans and Worksheets for Algebra II
Lesson Plans and Worksheets for all Grades
More Lessons for Algebra
Common Core For Algebra
The Definition of a Parabola
Student Outcomes
- Students model the locus of points at equal distance between a point (focus) and a line (directrix). They construct a parabola and understand this geometric definition of the curve. They use algebraic techniques to derive the analytic equation of the parabola.
New York State Common Core Math Algebra II, Module 1, Lesson 33
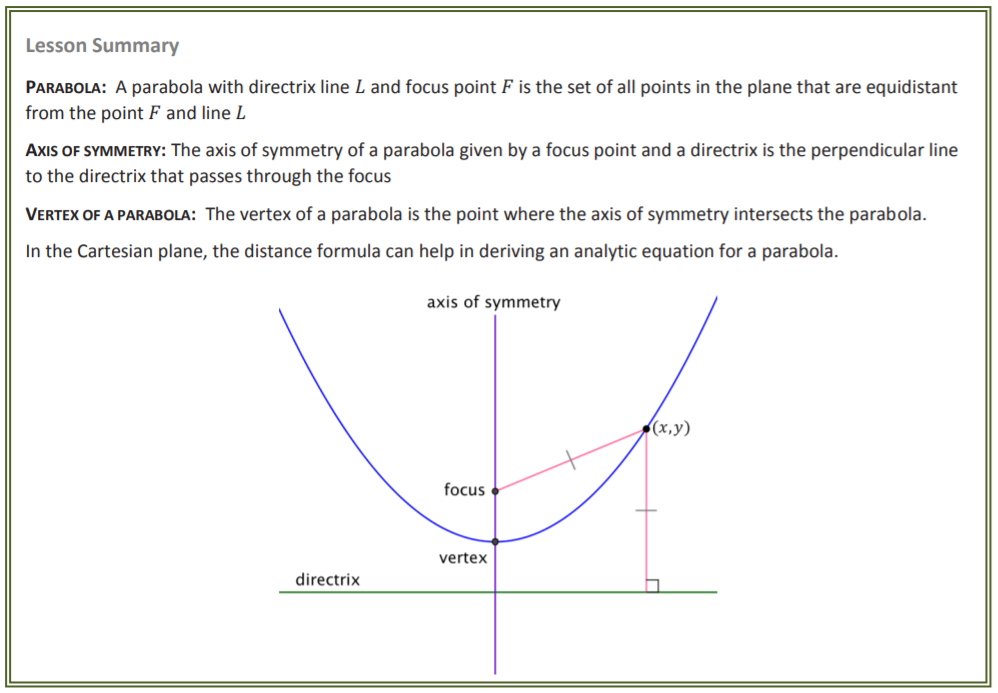
The following diagram shows the locus definition of a parabola. Scroll down the page for more examples and explanations about parabolas.
Classwork
Opening Exercise
Suppose you are viewing the cross-section of a mirror. Where would the incoming light be reflected in each type of design? Sketch your ideas below
Discussion: Telescope Design
When Newton designed his reflector telescope, he understood two important ideas. Figure 1 shows a diagram of this type of telescope.
- The curved mirror needs to focus all the light to a single point that we will call the focus. An angled flat mirror is placed near this point and reflects the light to the eyepiece of the telescope.
- The reflected light needs to arrive at the focus at the same time. Otherwise, the image is distorted.
Definition: A parabola with directrix 𝐿 and focus point 𝐹 is the set of all points in the plane that are equidistant from the point 𝐹 and line 𝐿.
Figure 2 to the right illustrates this definition of a parabola. In this diagram, 𝐹𝑃1 = 𝑃1𝑄1, 𝐹𝑃2 = 𝑃2𝑄2, 𝐹𝑃3 = 𝑃3𝑄3 showing that for any point 𝑃 on the parabola, the distance between 𝑃 and 𝐹 is equal to the distance between 𝑃 and the line 𝐿.
All parabolas have the reflective property illustrated in Figure 3. Rays parallel to the axis reflect off the parabola and through the focus point, 𝐹. Thus, a mirror shaped like a rotated parabola would satisfy Newton’s requirements for his telescope design.
Figure 4 below shows several different line segments representing the reflected light with one endpoint on the curved mirror that is a parabola and the other endpoint at the focus. Anywhere the light hits this type of parabolic surface, it always reflects to the focus, 𝐹, at exactly the same time.
Figure 5 shows the same image with a directrix. Imagine for a minute that the mirror was not there. Then, the light would arrive at the directrix all at the same time. Since the distance from each point on the parabolic mirror to the directrix is the same as the distance from the point on the mirror to the focus, and the speed of light is constant, it takes the light the same amount of time to travel to the focus as it would have taken it to travel to the directrix. In the diagram, this means that 𝐴𝐹 = 𝐴𝐹𝐴, 𝐵𝐹 = 𝐵𝐹𝐵, and so on. Thus, the light rays arrive at the focus at the same time, and the image is not distorted.
Example: Finding an Analytic Equation for a Parabola
Given a focus and a directrix, create an equation for a parabola.
Focus: 𝐹(0,2)
Directrix: 𝑥-axis
Parabola:
𝑃 = {(𝑥, 𝑦)| (𝑥, 𝑦) is equidistant from 𝐹 and the 𝑥-axis.}
Let 𝐴 be any point (𝑥, 𝑦) on the parabola 𝑃. Let 𝐹′ be a point on
the directrix with the same 𝑥-coordinate as point 𝐴.
What is the length 𝐴𝐹′?
Use the distance formula to create an expression that represents the length 𝐴𝐹<br
Create an equation that relates the two lengths, and solve it for 𝑦.<br
Verify that this equation appears to match the graph shown.
Exercises
- Demonstrate your understanding of the definition of a parabola by drawing several pairs of congruent segments given the parabola, its focus, and directrix. Measure the segments that you drew to confirm the accuracy of your sketches in either centimeters or inches.
- Derive the analytic equation of a parabola given the focus of (0,4) and the directrix 𝑦 = 2. Use the diagram to help
you work this problem.
a. Label a point (𝑥, 𝑦) anywhere on the parabola.
b. Write an expression for the distance from the point (𝑥, 𝑦) to the directrix.
c. Write an expression for the distance from the point (𝑥, 𝑦) to the focus.
d. Apply the definition of a parabola to create an equation in terms of 𝑥 and 𝑦. Solve this equation for 𝑦
e. What is the translation that takes the graph of this parabola to the graph of the equation derived in Example 1?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.