Positive and Negative Square Roots

Positive and Negative Square Roots
Every Positive Number Has Two Square Roots.
For any positive real number x, there exist two square roots:

1. Principal (Positive) Square Root: Denoted as √x
2. Negative Square Root: Denoted as −√x

For example, there are actually two numbers that are the square root of 25.
The principal square root or positive square root is 5, but there is also the negative square root which is −5. This is because 5² = 25 and (-5)² = 25.

The principal square root of 0 is 0. Notice that 0 only has one square root.

The following table gives a summary comparing positive and negative square roots. Scroll down the page for more examples and solutions.

 

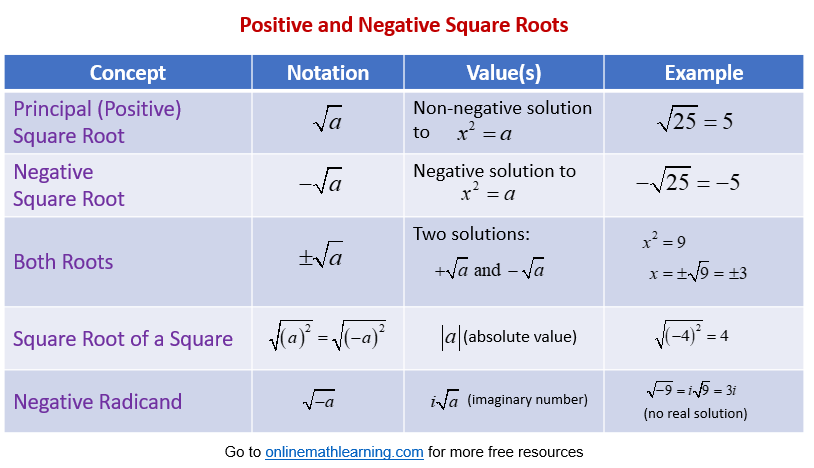
Note

1. The radical symbol (√) alone refers only to the positive root or principal square root.
2. When solving equations consider both the positive and negative square roots.

In this video, we will look at what is the principal square root of a nonnegative number?
The principal square root of a nonnegative real number is its nonnegative square root. The radical symbol refers specifically to the principal square root of a number. Thus, √16 = 4, even though 16 has two square roots, √16 = 4 because 4 is the principal square root. The negative square root is -4.

Principal Square Roots
This video explains what is meant by the principal square root and when to use it.

• Show Video

Positive and Negative Square Roots
How to find square roots of integers.

• Show Video

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.